 Na imagem visualizamos o logotipo do projeto 'MatematiZou', escrito com letras de forma na cor verde-azulada. A letra “Z” está na cor branca dentro de um hexágono com pontas arredondadas preenchido na mesma tonalidade de cor do restante das letras.  Na imagem temos um mini caminhão branco de madeira, cuja caçamba é azul escura e está escrito em letras brancas “UFABC”. As rodas do caminhão são vermelhas e quadradas. Cada par de rodas do caminhão está em cima de uma pista com ondulações.  Na imagem, há várias pessoas participando do evento “UFABC para todos” no Ginásio da UFABC campus Santo André. Algumas pessoas estão ao redor de uma mesa com jogos que incluem copos, mapas, tabuleiro de xadrez, entre outros, e outras, estão vendo as exposições espalhadas por todo o ambiente.](https://matematizou.gradmat.ufabc.edu.br/files/LogoMatematizouTeal.png)
Challenge 1. Given 2 points inside this disk, what are the paths on which walkers take fewer steps between the points? In other words, what are the paths of minimum length?
Answer:
The objective of this challenge is to describe qualitatively the shortest paths (geodesics) for the inhabitants of the disk.
Unlike the Euclidean plane, we cannot consider a straight line segment as the shortest distance between the points. Note that as walkers move towards the center of the disk, their steps become longer, resulting in wider strides. Therefore, we can assert that paths tending towards the center are shorter, forming a curve directed towards the center. Indeed, such behavior is observable (see the image below).
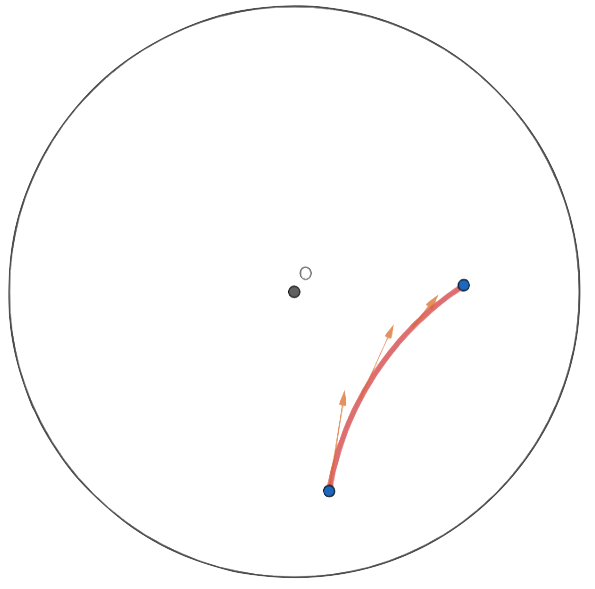
It is not within the scope of this activity to show what the paths in this space will be. However, we affirm that they fall into two categories: if the straight line determined by the two points intersects the center, then the straight segment will be the geodesic. When this does not occur, it will be an arc of a circumference orthogonal to the disk. See the section “Construction of the Poincaré Disk” to understand how we can obtain such paths.
Challenge 2: Consider that a walker takes steps of size 1/2 when starting their journey from the center of a disk with radius R=1. How many steps will it take for them to reach the boundary delimited by the circumference? Would it be possible for a walker from the disk to cross the boundary?
Hint: The Euclidean distance r_n from the center to the n-th step is given by r_n= \frac{3^n-1}{3^n+1}.
* The hint above utilizes the fact that if r is the Euclidean distance between the center and a point on the disk, then the distance for inhabitants in the disk is given by ln(\frac{1+r}{1-r}), which must be subsequently rescaled to the step size. Consequently, each step has a length of ln(3) within the disk (i.e., for its inhabitants), which corresponds to us, external observers, as a length of 1/2 of the Euclidean radius on the walker’s first step.
Solution:
We will use the hint to solve the problem. The walker will reach the boundary on the n-th step when r_{n-1}<1 and r_n\geq 1 (assuming that the n-th step may be less than one full step).
Therefore, we seek n such that r_n= \frac{3^n-1}{3^n+1} \geq 1. However, if we suppose this statement to be true, we would have 3^n-1 \geq 3^n+1, which implies -1 \geq 1, which is absurd. Therefore, the walker never reaches the boundary in finite time. In other words, the segment between the center of the disk and the boundary is infinite.
The above answer also guarantees that the walker does not cross the boundary. However, suppose additionally that this individual is already at the boundary. Then the length of their legs is zero, as it follows the proportion of 1^2-1^2=0. Therefore, the answer is always negative for this item.
A curious fact is that this problem can be compared to Zeno’s paradox. However, in this case, the geometry is different, causing the space to dilate from the perspective of the inhabitants of the disk, and the problem is modified by considering the number of steps instead of the space itself.
