Historical Background
The Poincaré Disk is a visual representation of hyperbolic geometry developed by the French mathematician Henri Poincaré in the late 19th century. The motivation behind this representation arose from the quest to understand and explore non-Euclidean geometries, which were a paradigm shift from Euclidean classical geometry.
This activity has been designed with the purpose of introducing the reader to non-Euclidean geometry through a visual and interactive approach. Our goal is to assist the reader in comprehending the unique properties of hyperbolic geometry, utilizing the Poincaré Disk as a visualization tool. Hyperbolic geometry emerges from an axiom where, given a point and a line in this space, there exist more than one (infinite) lines passing through this point that do not intersect with the provided line.
The Poincaré Disk played a fundamental role in understanding non Euclidean geometries by providing a visual representation for hyperbolic geometry. The disk model, originally proposed by Bernhard Riemann during a lecture in 1854 (which was later published in 1868), gained more prominence through an article by Eugenio Beltrami in the same year. However, it was Henri Poincaré who incorporated the model into a comprehensive treatment of hyperbolic, parabolic, and elliptic functions in his work of 1882. Recognition of the model, however, came with Poincaré’s philosophical work in 1905, “Science and Hypothesis,” in which he introduced a conceptual universe now known as the Poincaré disk. Within this region, space is described by Euclidean elements, yet intriguingly, for inhabitants of this disk, the geometry is hyperbolic, presenting a fascinating connection between the two geometries.
Activity Description
Below, we outline the activities where we initially propose an intuition about how distances behave distinctly for inhabitants of the disk. Subsequently, we propose the construction of the Poincaré disk.
Walkers in the Poincaré Disk
Consider inhabitants living within an area bounded by a circumference. Something very peculiar happens to them: their legs continuously shrink as they move away from the center of the circumference. More specifically, consider that the circumference has a radius R, and when the leg is at a distance r from the center of the circumference, the length of the walker’s leg will be proportional to R²-r² of its value at the center. For the walkers, distances within this disk are measured by the number of steps they need to move from one point to another.

Challenges:
- Given 2 points inside this disk, what are the paths on which walkers take fewer steps between the points? In other words, what are the paths of minimum length?
- Consider a walker taking steps of size \frac{1}{2} when they start their walk at the center of the disk with a radius R=1. How many steps will it take for them to reach the boundary delimited by the circumference? Would it be possible for a walker from the disk to cross the boundary?
Hint: The Euclidean distance r_n from the center to the n -th step is given by r_n= \frac{3^n-1}{3^n+1}.
The above hint utilizes the fact that if r is the Euclidean distance between the center and a point in the disk, then the distance for inhabitants in the disk is given by ln(\frac{1+r}{1-r}), , which must be subsequently rescaled to the step size.
Construction of the Poincaré Disk (Do it at home/school)
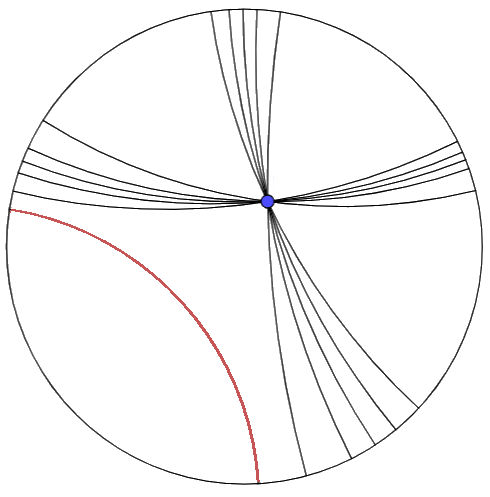
We can construct the Poincaré disk by describing the behavior of lines in space. As seen in the activity of walkers in the disk, the distance from the center to the boundary will be infinite for the inhabitants of this space. However, lines are defined by the shortest paths in the disk, and, in a simplified manner, we will see how to construct the shortest paths in this geometry.
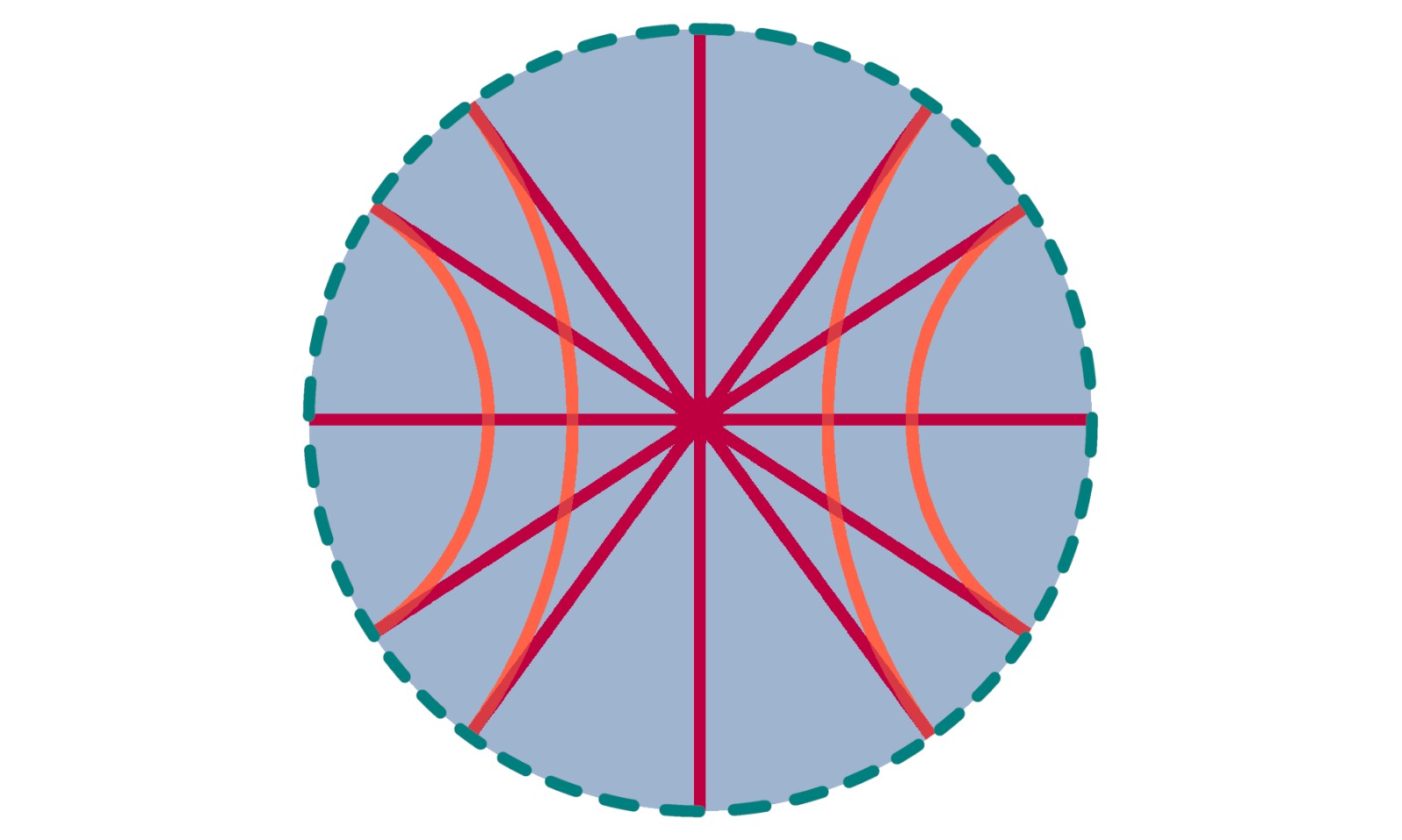
In summary, the shortest paths will be lines that intersect the center of the circumference and orthogonal circles, that is, arcs that belong to circles whose tangents intersect perpendicularly to the boundary (tangents) of the disk. The shortest paths are called geodesics.
Before we start the construction, let’s remember how we define the inversion of points by a circumference.
Point Inversion
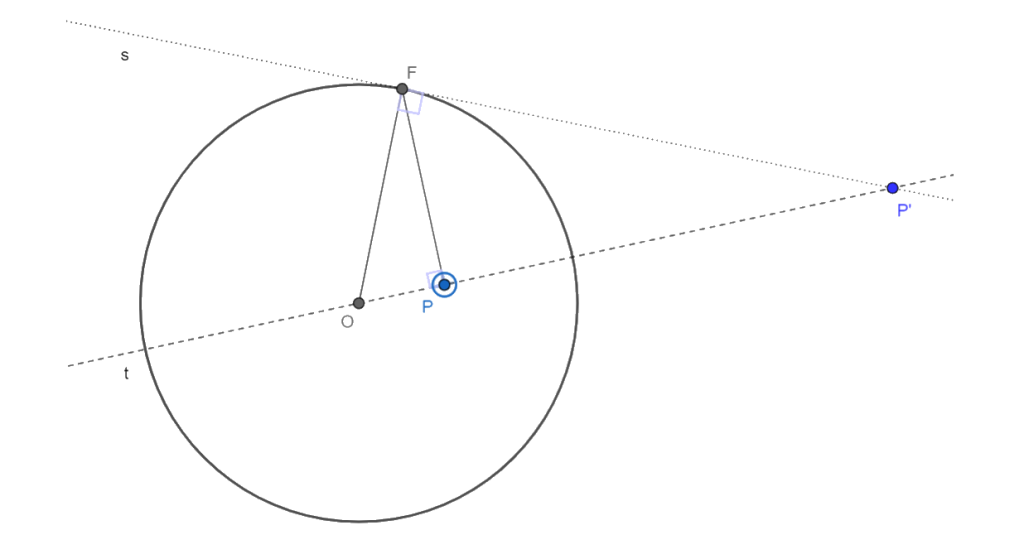
- Let P be a point inside a circumference with center O, and let t be the line containing O and P.
- Consider F to be a point on the circumference that belongs to the line perpendicular to t intersecting point P.
- Let s be the line perpendicular to segment OF.
- The point P’ is the inversion of P by the circumference when P’ is the point of intersection between the lines s and t.
Paths in the Poincaré Disk
Consider P and Q as points inside the disk. Let l be the line determined by P and Q. If O belongs to l, then the shortest path between P and Q is the line segment PQ.
Otherwise, we perform the following construction using ruler and compass:
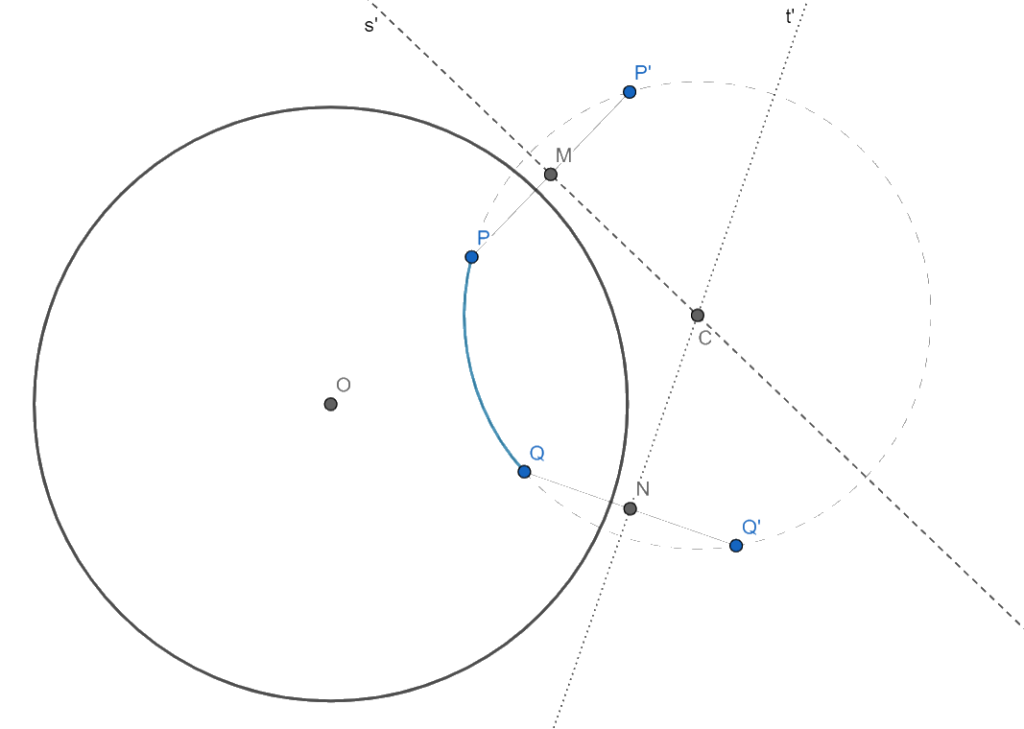
- Let P’ and Q’ be the inversion of P and Q by the disk.
- Consider M and N as the midpoints of PP’ and QQ’, respectively.
- Let s’ and t’ be the lines perpendicular to PP’ and QQ’.
- Define C as the point of intersection between s’ and t’.
- The arc of the circumference between P and Q with center at C is the geodesic between P and Q in the Poincaré disk.
Properties of the Disk
This disk allows us to verify several properties of hyperbolic geometries. For example, we can construct a Khayyam-Saccheri quadrilateral. Despite this quadrilateral having three right angles, the fourth internal angle will be acute. Consequently, the sum of the internal angles will be less than 2\pi.
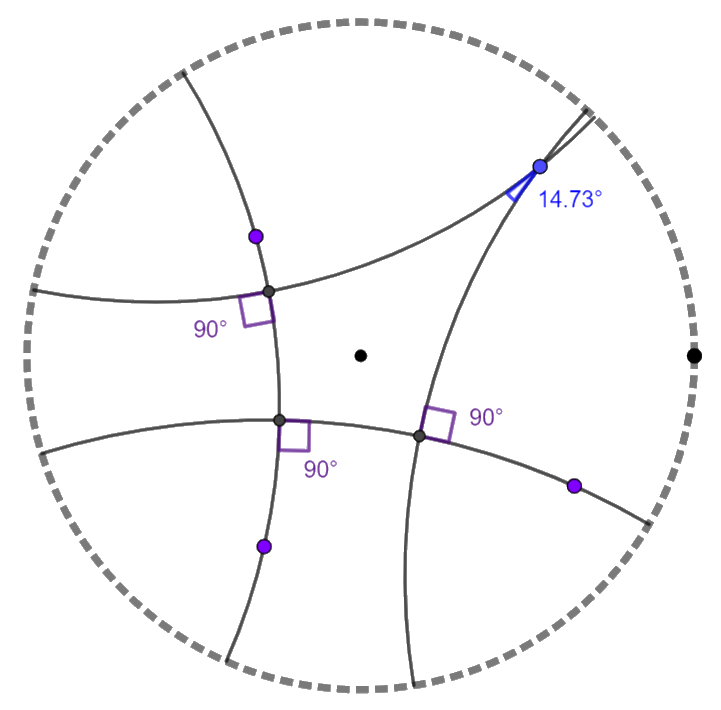
Since non-Euclidean geometry is based on disregarding the parallel postulate, we have evidence of the existence of multiple parallel lines between a line and a point.
Learn More
Explore more properties of hyperbolic geometry in the Poincaré disk in the following application https://www.geogebra.org/m/mpzwcqka (provided by Guilherme A. Rink).
Another option would be to use a more constructive application like the one available athttps://www.geogebra.org/m/R5e9AggU (in English)
In the following video, we can see a representation of the disk with cars living in this space (instead of walkers), thus associating with a projective property between a surface and the disk https://youtu.be/nu4mkwBEB0Y?feature=shared
This model has also been explored in the arts, especially by Escher in some works, see https://mathstat.slu.edu/escher/index.php/Circle_Limit_Exploration
If you are interested in learning more about the theory behind the Poincaré disk with advanced mathematics (upper-level), we recommend the text “Poincaré and his disk” by Étienne Ghys (in English) https://perso.ens-lyon.fr/ghys/articles/Poincarediskenglish.pdf
 Na imagem visualizamos o logotipo do projeto 'MatematiZou', escrito com letras de forma na cor verde-azulada. A letra “Z” está na cor branca dentro de um hexágono com pontas arredondadas preenchido na mesma tonalidade de cor do restante das letras.  Na imagem temos um mini caminhão branco de madeira, cuja caçamba é azul escura e está escrito em letras brancas “UFABC”. As rodas do caminhão são vermelhas e quadradas. Cada par de rodas do caminhão está em cima de uma pista com ondulações.  Na imagem, há várias pessoas participando do evento “UFABC para todos” no Ginásio da UFABC campus Santo André. Algumas pessoas estão ao redor de uma mesa com jogos que incluem copos, mapas, tabuleiro de xadrez, entre outros, e outras, estão vendo as exposições espalhadas por todo o ambiente.](https://matematizou.gradmat.ufabc.edu.br/files/LogoMatematizouTeal.png)

