The problem of the three cards (Solution)

Let’s number the cards and faces as following:

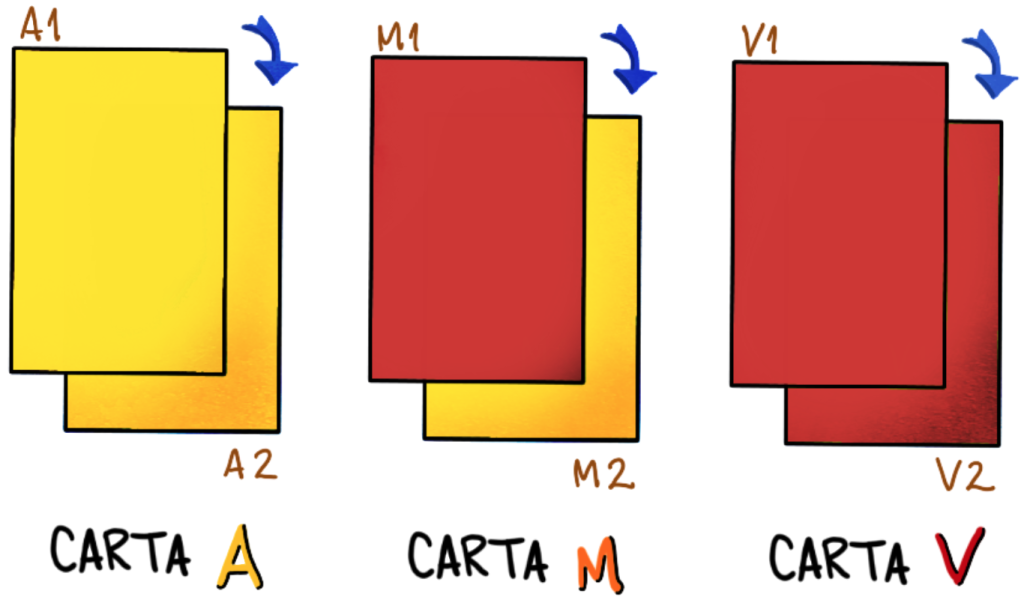
• Card A (yellow)    with faces: Yellow   (A1) – Yellow (A2) 
• Card M (mixed) with faces: Red (M1) – Yellow  (M2)
• Card V (reed)   with faces: Red (V1) – Red (V2)

In this context, consider any card C as one of the cards A, M, or V. We assume that (Ci, Cj) represents the player seeing face Ci while keeping face Cj hidden; if it were the same card but the player saw face Cj, we call it (Cj, Ci).

Then, all possible combinations are given by the following set:

{(A1,A2), (A2,A1), (M1,M2), (M2,M1), (V1,V2), (V2,V1)}.

Now, assuming that the player is seeing a yellow face, we have that the space of possible events (in this case, we can explain a little about Conditional Probability) would be the total Sample Space without the faces of the completely red card, i.e.:

{(A1,A2), (A2,A1), (M2,M1)}

Clearly, we will have two situations with the hidden yellow face and one with the hidden red face. Since there is no bias in the draw, meaning the events are equiprobable, the chance of the hidden face being red, given that the displayed face is yellow, reduces to ⅓.

Comparing with the Monty Hall problem

The explanation above is straightforward and clear. However, the fact that the result presents probabilities similar to the Monty Hall problem, which can be counterintuitive, allows us to compare them side by side.

Consider that we have 3 doors A, M, and V representing each card with the same name. The visible side of the card is equivalent to the host opening the door with two different colors from the revealed color (the door without the prize). Therefore, the only choice of door allowed before the revelation would be door M (with two different colors). Thus, switching doors is equivalent to choosing the card with both sides having the same revealed color!

Note that, in this case, the initial choice of door M is indeed mandatory, which does not alter the probability of ⅓ of it being the card drawn.