Visual Topology

Motivation

The main objective of this activity is to present mathematical experiments to the audience using visual tools [3]. Our basic topological experiment will help the audience rediscover intriguing mathematical properties. This experiment is based on well-known topological objects such as the Möbius strip and the Klein bottle.

In this exhibition, we aim to showcase the beauty of topology to a general audience using simple terminology. Even though the results may not be intuitive, the audience can pose many interesting questions

Möbius Strip

A Möbius strip (or Möbius band) is a surface with a single twist that has exactly one edge and exactly one face.

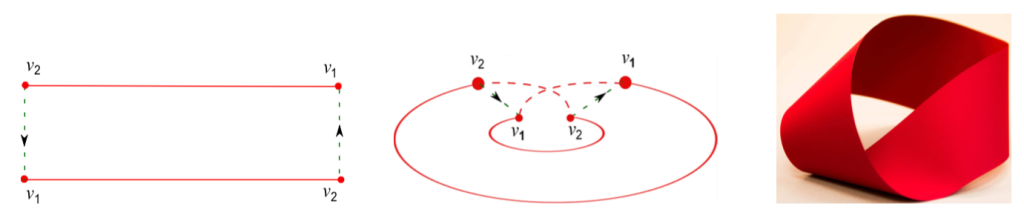
To construct a Möbius strip, we begin by taking a long rectangular strip of paper and labeling the ends of its edges with v_1 e v_2 so that no two consecutive ends have the same label (see Figure 1(a)). Note that the arrows in Figure 1(a) go from v_2 to v_1 (where v_1 is the head and v_2 the tail of the arrows); this indicates how the ends of the rectangular strip should be glued in the next step. The Möbius strip is obtained by gluing the short edges of this rectangle, i.e., identifying head with head (v_1 with v_1) and tail with tail (v_2 with v_2) of the arrows. The two ends labeled with v_1 will overlap, and similarly, the ends labeled v_2 will overlap in the final step, as seen in Figure 1(b). Additionally, it should be noted that the dashed lines in Figure 1(b) are virtual; we show them to indicate that the two heads of the arrows marked with v_1 are, in fact, the same. Similarly, the two tails labeled as v_2 are the same.

Question 1: Run your fingers along the edge from a fixed point (make sure it’s on the edge). Is it possible to return to the fixed point without lifting your fingers at any point?

• Is it possible to return to the fixed point without lifting your fingers at any point?
• What is the total number of edges the strip can have?

Question 2: Hold the Möbius strip between two fingers halfway along the edge (index finger on top and thumb below). Mark a point Q_1 next to one finger and Q_2 next to the other finger (see Figure).

• Is it possible to move one finger from Q_1 to Q_2 through the center of the strip without lifting the finger at any point?
• How many faces are there on the Möbius strip?

Cutting the Möbius Strip

Cut the Möbius strip along its centerline (as described in the figure).

• How many twists will result after the cut?
• How many strips will result after the cut?
• How many faces will result after the cut?
  

Cutting the Möbius Strip Again

Cut the strip resulting from the previous experiment in half.

• How many twists will result after the cut?
• How many strips will result after the cut?
• How many faces will result after the cut?

Reference

1. S. Barr, Experiments in Topology, Reprint of the 1964 original. Dover Publications,
   Inc., Mineola, NY, 1989.
2. D. Davis, Algebraic Topology -There’s an App for That, Math Horizons, September
   2011.
3. R. Flórez and A. Mukherjee, Classroom experiences in introducing students to conjectures, exploration and visual proofs using experiments on the mobius strip. PRIMUS. 30.1 50-66, 2020. A version in PRIMUS.
4. J. Tanton, A dozen questions about a donut, Math Horizons, November 1998.