 Na imagem visualizamos o logotipo do projeto 'MatematiZou', escrito com letras de forma na cor verde-azulada. A letra “Z” está na cor branca dentro de um hexágono com pontas arredondadas preenchido na mesma tonalidade de cor do restante das letras.  Na imagem temos um mini caminhão branco de madeira, cuja caçamba é azul escura e está escrito em letras brancas “UFABC”. As rodas do caminhão são vermelhas e quadradas. Cada par de rodas do caminhão está em cima de uma pista com ondulações.  Na imagem, há várias pessoas participando do evento “UFABC para todos” no Ginásio da UFABC campus Santo André. Algumas pessoas estão ao redor de uma mesa com jogos que incluem copos, mapas, tabuleiro de xadrez, entre outros, e outras, estão vendo as exposições espalhadas por todo o ambiente.](https://matematizou.gradmat.ufabc.edu.br/files/LogoMatematizouTeal.png)
What history is this?
Have you ever tried to color the states of a country utilizing at most four different colors in such a way that the neighbor states do not get painted in the same color? It is understood that neighbor states are those that in a map they border each other. In 1852, Francis Guthrie made such a task with the England district’s map. As such he conjectured that any map could be colored using only four different colors. Still in 1852, very excited knowing this conjecture, De Morgan sent a letter explaining it to Hamilton but he did not find this problem very interesting.
Many mathematicians ventured to study Guthrie’s conjecture, but a proof of its validity was only given in 1976 by Appel and Haken, having been necessary more than a thousand hours of computer calculations. In 1994, at the International Mathematical Congress in Zurich, Seymour, Robertson, Sanders and Thomas presented a new demonstration using computers, but with more simplified calculations. To date, there is no known demonstration of the four-color theorem without the aid of computers. However, many applications, variations and generalizations of the problem have emerged in recent decades.
Activity description
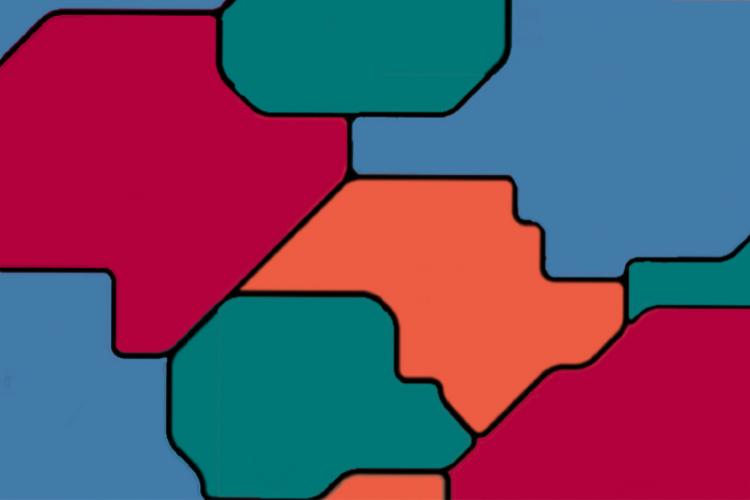
You have to color all the countries of the map, shown below, using only four colors in such a way that their neighbor does not have the same colors.
Created with Geogebra. Adapted from Marco A. Manetta
You have to color all the regions below using only four colors as such that no region have the same neighbor’s color (all the regions border must not have the same color). Click first in a color and next to a region.
Created with Geogebra. Adapted from Marco A. Manetta
Learn more
- Gerhard Ringel. Map Color Theorem, New York–Berlin: Springer-Verlag, 1974.
- Kenneth Appel, Wolfgang Haken. The Solution of the Four-Color-Map Problem, Scientific American, Vol. 237, No. 4 (October 1977), pp. 108-121.
- John Mitchem. On the History and Solution of the Four-Color Map Problem, The Two-Year College Mathematics Journal, Vol. 12, No. 2 (Mar., 1981), pp. 108-116.
How to do it at home/school
First variation:
This activity must be applied to two players. Each one receives a map and four pencils in the colors red, yellow, blue and green. The objective is to color the map using all four colors and no neighbors, the border of the regions, can have the same color. See who’s correctly completed the task.
Second variation:
An alternative to the game is to take the following pieces made from wood, cardboard or EVA:
- Six rectangular pieces with sides measuring 5 cm and 15 cm, being two yellow, two blue and two green;
- Six rectangular pieces with sides measuring 5 cm and 10 cm, being two blue, two red and two green;
- Six squared pieces with sides measuring 5 cm, being three blue, two red and one yellow.
The aim is to build a square using all the pieces and no border can have the same color of contact. The winner is the person who completes it correctly.
