Stereographic Projection

Once a point X is fixed on a sphere, stereographic projection consists of projecting, from X, the entire sphere onto a plane. Usually, the north pole of the sphere, denoted by N, is taken as the fixed point. In this case, for each point P on the sphere, different from the north pole N, the image of P by the stereographic projection, denoted by P′, is the point of intersection of the ray that joins N and P with the chosen projection plane. When considering stereographic projection relative to the north pole, the following two choices are generally made for the projection plane:

1. The projection plane touches the sphere at its south pole, denoted by S, as illustrated in Figure 1.

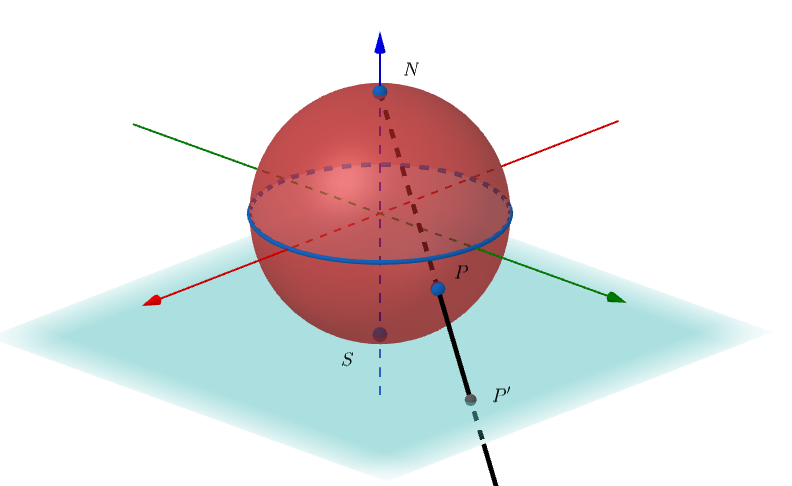
Can you imagine what the image of the sphere’s equator will be through stereographic projection? Think for a few moments before viewing the next image.

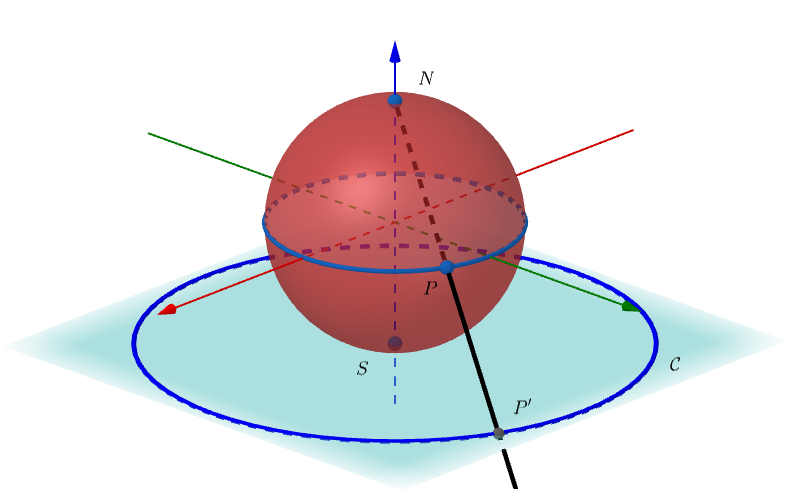
When the projection plane touches the sphere at the South Pole, the image of the sphere’s equator by stereographic projection is also a circle C which is contained in the projection plane and whose center is the point S, as illustrated in Figure 2. Note that, in this way, the northern hemisphere of the sphere will be projected onto the outside of C in the projection plane, while the southern hemisphere over the interior of C on the projection plane.

2. The projection plane contains the equator of the sphere, as illustrated in Figure 3.

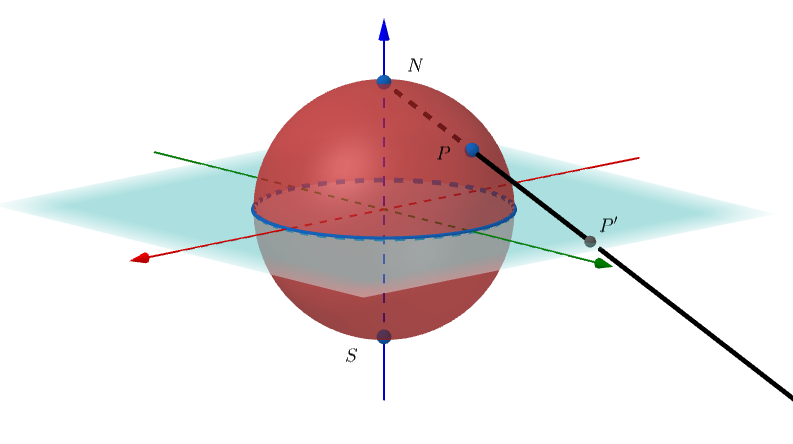
In this case, the equator of the sphere remains fixed by the stereographic projection. The northern hemisphere is carried by stereographic projection on the outside of the sphere’s equator in the projection plane, while the southern hemisphere is carried on the inside. To which point is the south pole led?

Applications

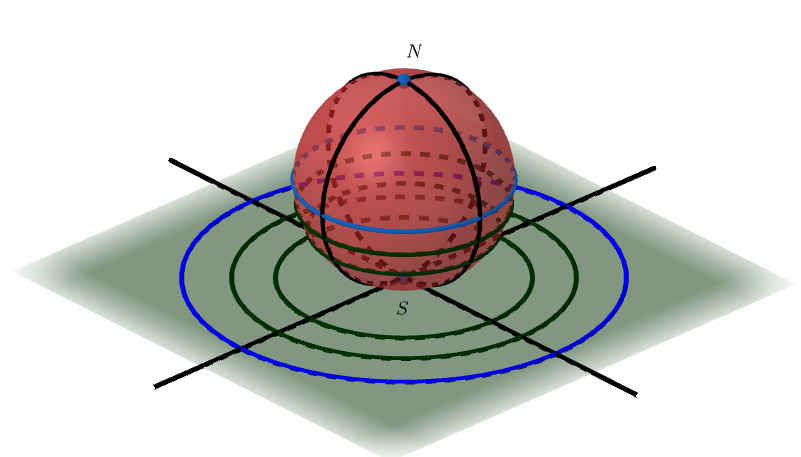
A well-known application of stereographic projection is in Nautical Cartography. In this case, the projection plane is tangent to the earth’s surface at one of the poles (as in Case 1 above), so that the flat representation of a polar region can be obtained without many distortions. Think for a moment about the following situation: considering the stereographic projection from the north pole onto the plane that touches the Earth at the south pole, what will the Earth’s parallels and meridians look like in the projection?

Figure 4 illustrates this situation.

Imagine what the geographic map of the Earth would look like if stereographic projection were used. You will see the map of the northern hemisphere obtained through stereographic projection from the south pole onto the plane that touches the Earth at the north pole by accessing the link {https://encurtador.com.br/kxJPU}

Another application that has been adopted in recent years is the production of photographs using stereographic projection. Many of them can be found and viewed online, such as those accessed via the links {https://encurtador.com.br/kDF37} and {https://encurtador.com.br/ckpuw}

How to do it at home/at school?

A possible activity on stereographic projection that can be carried out at home or at school uses only a (hollow) polystyrene ball, a sheet of paper, a barbecue stick and a pencil. The paper is placed on a table and the polystyrene ball is placed on the paper, so that both do not slide. On the polystyrene ball, some points are marked, different from the north pole of the ball. Then, from the north pole, use a barbecue stick to pierce the polystyrene ball at the chosen points. With the pencil, mark the points where the stick touches the paper. The points marked on the sheet of paper are the images through the stereographic projection of the points marked on the polystyrene ball.

Learn more

To learn a little more about stereographic projection, access the following references:

• Gazeta de Matemática. Available at https://gazeta.spm.pt/get?gid=168 Access on: 21/08/2023.

• José M. S. dos Santos e Ana M. D. Breda. A projeção estereográfica no GeoGebra. 1ª. Conferência Latino Americana de GeoGebra. ISSN 2237- 9657, pp.AA-BB, 2011.