 Na imagem visualizamos o logotipo do projeto 'MatematiZou', escrito com letras de forma na cor verde-azulada. A letra “Z” está na cor branca dentro de um hexágono com pontas arredondadas preenchido na mesma tonalidade de cor do restante das letras.  Na imagem temos um mini caminhão branco de madeira, cuja caçamba é azul escura e está escrito em letras brancas “UFABC”. As rodas do caminhão são vermelhas e quadradas. Cada par de rodas do caminhão está em cima de uma pista com ondulações.  Na imagem, há várias pessoas participando do evento “UFABC para todos” no Ginásio da UFABC campus Santo André. Algumas pessoas estão ao redor de uma mesa com jogos que incluem copos, mapas, tabuleiro de xadrez, entre outros, e outras, estão vendo as exposições espalhadas por todo o ambiente.](https://matematizou.gradmat.ufabc.edu.br/files/LogoMatematizouTeal.png)
To simplify the resolution of the challenge, it is common in mathematics to transform a problem into another equivalent one, but with a simpler scenario. Initially, we will number the squares on the board as shown in the figure below:
Now observe that square 5 cannot be reached by the knight because there is no move that allows reaching it from the starting positions of the knights. Notice that the knight always moves in an L-shape, and if a knight were to move from any square to square 5, it could return to that square. However, from square 5, you cannot reach any other square using the L-shaped move.
Further observe that when leaving an odd-numbered square, you arrive at an even-numbered square, and when leaving an even-numbered square, you always arrive at an odd-numbered square. Let’s write down the possible moves for the knights initially on squares 1, 3, 7, and 9:
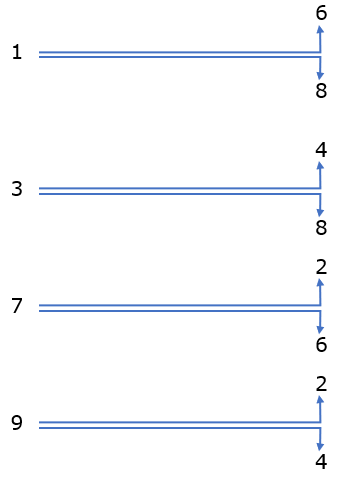
After numbering the squares on the board and then identifying the possible movements of each knight from a numbered square, we can transform the problem into a graph, a structure composed of points (vertices) and lines (edges), where each movement on the board corresponds to a movement in the graph and vice versa. Thus, each square will be represented by a vertex. Below, we have the graph for the initial position of the pieces:
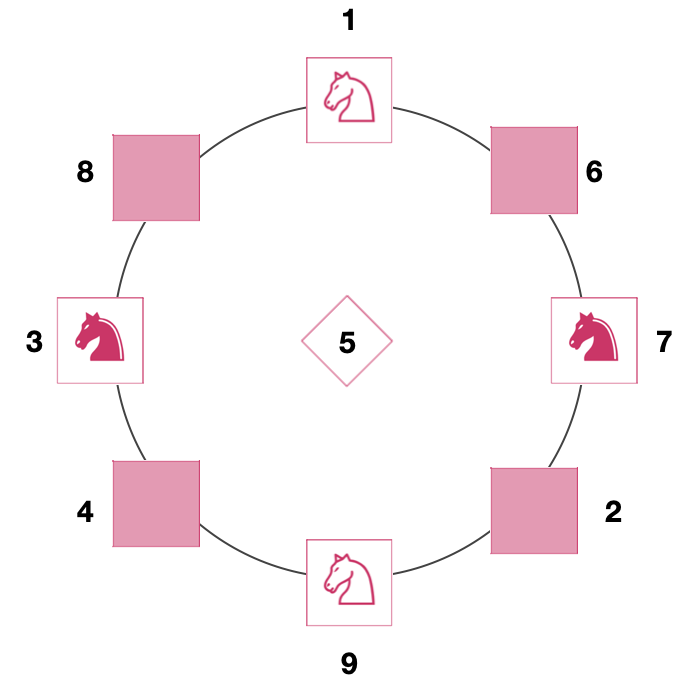
We can also consider the graph of the possible final positions given by the challenge:
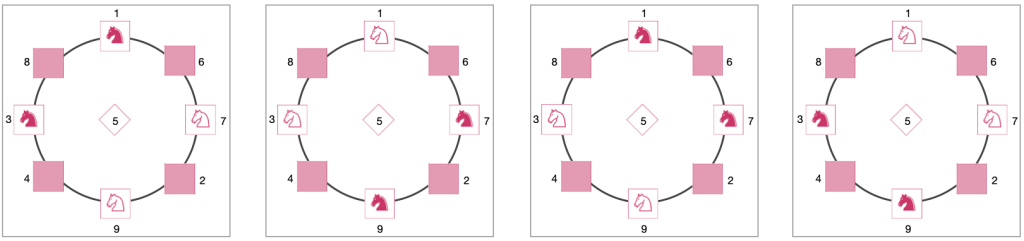
Now, the simplicity of the problem lies in realizing that each knight’s move on the board corresponds to a movement in the graph.
If you tried to solve the problem based on moves on the board, you might have noticed that it is very difficult to determine whether the problem has a solution or not.
If you tried to solve the problem based on moves on the board, you might have noticed that it is very difficult to determine whether the problem has a solution or not. However, when looking at the graph figures, note that the order in which the knights appear in the circle cannot be changed, as a knight of one color cannot jump over a knight of the other color in the circle. As a result, the proposed challenge has no solution.
