 Na imagem visualizamos o logotipo do projeto 'MatematiZou', escrito com letras de forma na cor verde-azulada. A letra “Z” está na cor branca dentro de um hexágono com pontas arredondadas preenchido na mesma tonalidade de cor do restante das letras.  Na imagem temos um mini caminhão branco de madeira, cuja caçamba é azul escura e está escrito em letras brancas “UFABC”. As rodas do caminhão são vermelhas e quadradas. Cada par de rodas do caminhão está em cima de uma pista com ondulações.  Na imagem, há várias pessoas participando do evento “UFABC para todos” no Ginásio da UFABC campus Santo André. Algumas pessoas estão ao redor de uma mesa com jogos que incluem copos, mapas, tabuleiro de xadrez, entre outros, e outras, estão vendo as exposições espalhadas por todo o ambiente.](https://matematizou.gradmat.ufabc.edu.br/files/LogoMatematizouTeal.png)
A question that always arises when we solve a problem like this is: can this idea be replicated for other versions of the same problem?
Consider, for example, that the ferryman needs to transport a rabbit, a goat, a wolf, a fox, and a basket of cabbages. The restrictions are as follows:
• The wolf and the fox eat the rabbit;
• The wolf and the fox also eat the goat;
• The goat and the rabbit eat the basket of cabbages.
The problem above can be represented by the following structure.
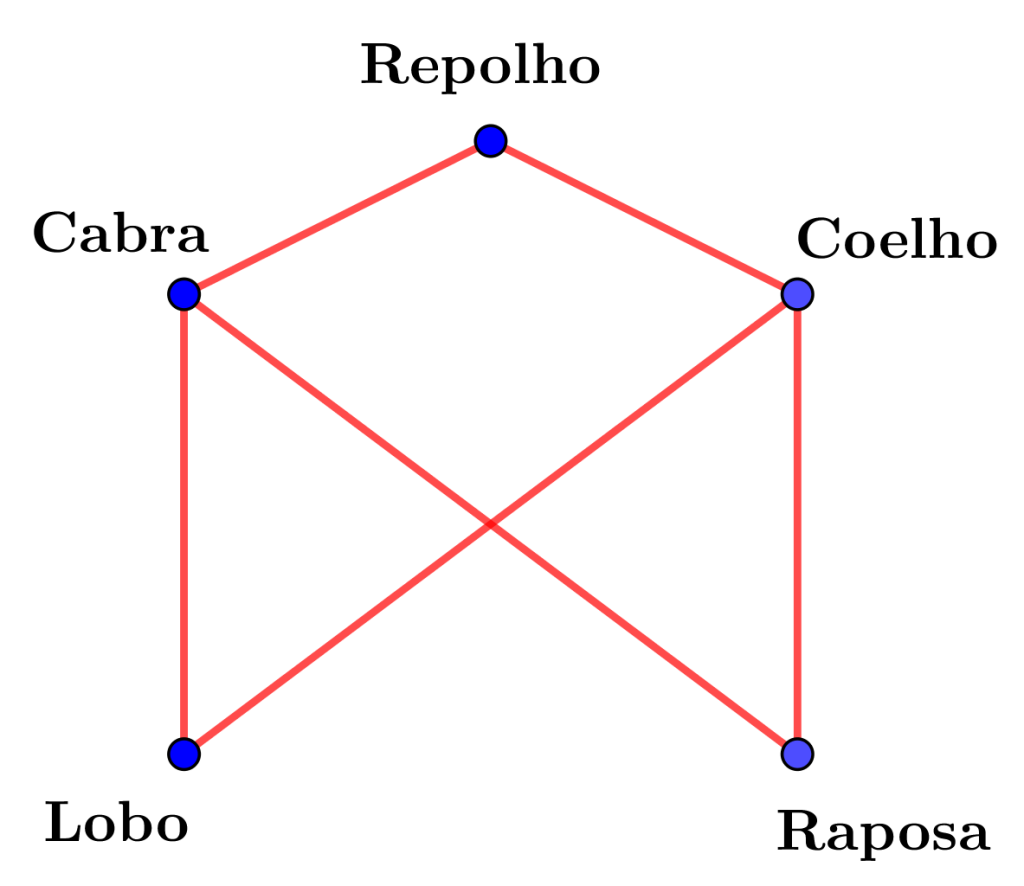
Looking at the structure depicted above, answer: Is it possible to cross all of them in a boat with only one seat? Take some time and think about the problem before proceeding.
To understand what’s happening, try to apply the same type of considerations to this problem as we did to the previous one.
Got it? If not, try asking yourself the following questions:
• In the original problem, the goat had a special role. What was that role?
• Can any passenger in this network play the same role?
• If not, what does that mean?
Take some time to ponder these questions before moving on.
The summarized answer is that a single-seat boat is too small for the ferryman to transport everyone safely! To see this, just go back to the above network and notice that removing only one passenger is not enough to resolve all conflicts! There will always be characters that can’t be together or alone.
Let’s change the question then!
What size of boat do we need to solve the problem? Could the ferryman transport everyone safely with a two-seat boat? Use the application below to try answering these questions. Hint: find a pair of characters that, when separated from the group, resolve the conflicts.
If you succeeded, congratulations!
The answer, analogous to the original problem, involves realizing that now the goat/rabbit pair, when separated from the group, avoids all conflicts. Thus, any solution must keep this pair apart from the others while transporting everyone or under the ferryman’s supervision.
1. Below, we provide a possible solution! Go back to the application and try replicating this solution, noting how the goat/rabbit pair is always separated from the others or, if they are with another character, they are under the ferryman’s supervision.
2. Place the goat/rabbit pair in the boat and take them to the other side of the river;
3. Return with the empty boat;
4. Put the wolf and the fox in the boat and take them to the other side of the river;
5. Leave the wolf and the fox on the shore and put the goat and rabbit in the boat;
6. Return with the goat/rabbit pair;
7. Leave the pair on the shore and put the cabbage in the boat;
8. Take the cabbage to the other side;
9. Return with the empty boat to fetch the goat/rabbit pair.
In the next level, inspired by the problem we just solved, we’ll present some questions that mathematicians often ask when confronted with this type of challenge. When you’re ready, just click the button below!
