A plank slides on wheels, always parallel and at the same distance from the base. However, the wheels are not round! What is happening?
The engineer Franz Reuleaux (19th century, German, but pronounced “roy-luh” with an “r” rolled and the first “o” pronounced like “aw”) developed various mechanisms for transforming motion.
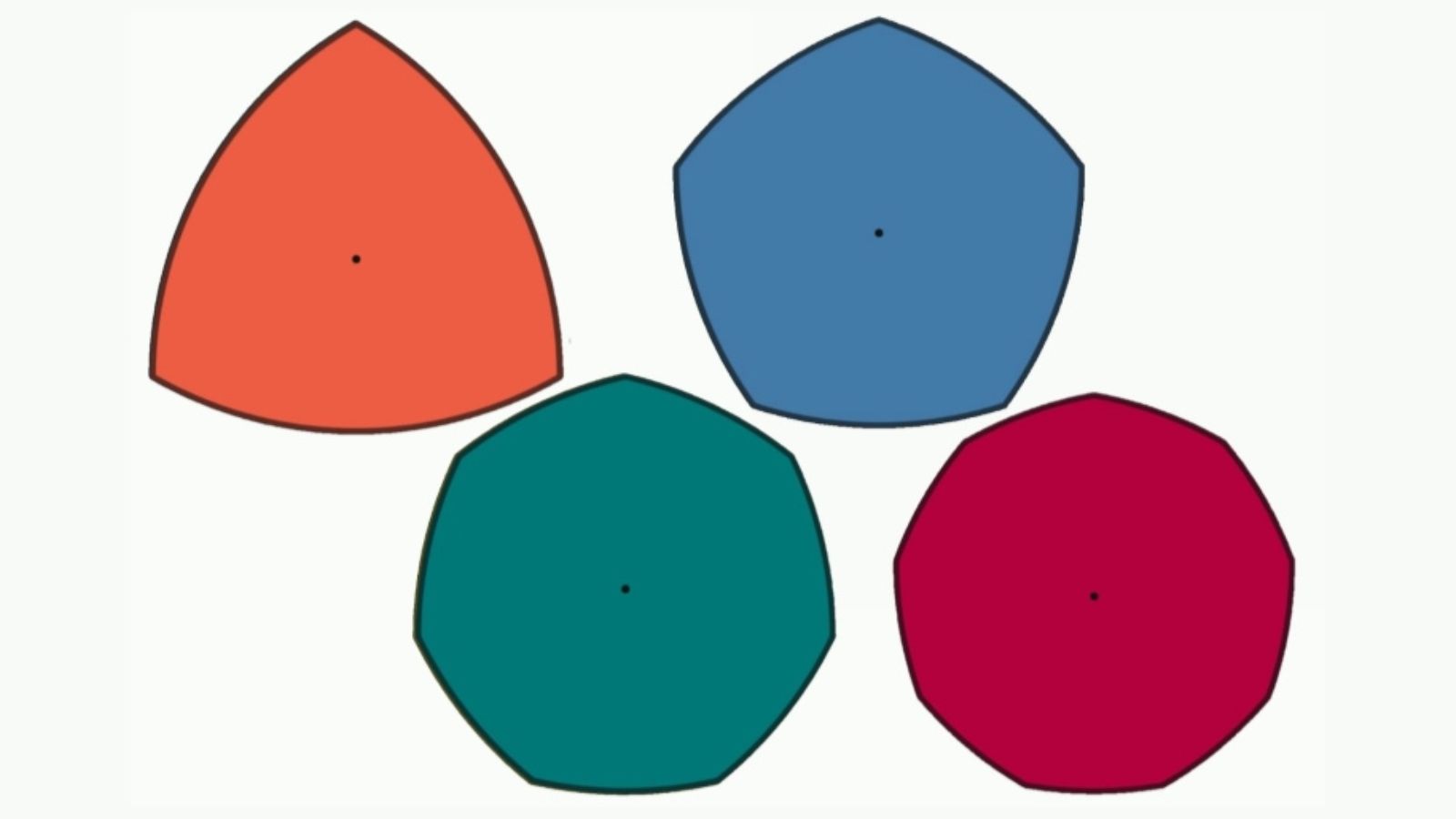
To construct a Reuleaux triangle, start with an equilateral triangle with sides of length L. With the center at each vertex, open the compass and describe the (smaller) arc of a circle passing through the other two vertices. The resulting closed curve has a “constant width” L, which is the distance between the two parallel tangents. The construction can be generalized to other polygons and (after some interventions) also to polyhedra.
Note that, as it rolls, the axis of the Reuleaux “wheel” goes up and down, causing a car with such wheels to vibrate on a flat road. On the other hand, in the case of the plank supported on cylinders with this cross-section, the rolling has two points of static equilibrium, one stable (with the lower axis and of practical interest) and the other unstable (with the higher axis).
Any curve of constant width can be inscribed in a square and rotate within it (with sliding), although, again, its center does not remain fixed. Some drills for creating polygonal holes are manufactured according to this principle.
Construction of the Polygon
Rotating Polygon
 Na imagem visualizamos o logotipo do projeto 'MatematiZou', escrito com letras de forma na cor verde-azulada. A letra “Z” está na cor branca dentro de um hexágono com pontas arredondadas preenchido na mesma tonalidade de cor do restante das letras.  Na imagem temos um mini caminhão branco de madeira, cuja caçamba é azul escura e está escrito em letras brancas “UFABC”. As rodas do caminhão são vermelhas e quadradas. Cada par de rodas do caminhão está em cima de uma pista com ondulações.  Na imagem, há várias pessoas participando do evento “UFABC para todos” no Ginásio da UFABC campus Santo André. Algumas pessoas estão ao redor de uma mesa com jogos que incluem copos, mapas, tabuleiro de xadrez, entre outros, e outras, estão vendo as exposições espalhadas por todo o ambiente.](https://matematizou.gradmat.ufabc.edu.br/files/LogoMatematizouTeal.png)

