Pi (π) – the number

Pi (π) is the most known mathematical constant in the world. Most scientists believe that the number Pi is the most intriguing and important number in maths. But, what is the meaning of the number Pi? It is an irrational number which has the value of 3.14159265358979323846… (And it goes on and on never to reach an end).

An Indian called Sharma Suresh Kumar owns the Guinness World Records for spelling the most quantities digits of Pi. She recited without error 70,030 digits in 17 hours and 14 minutes. The team that holds the record of most digits computationally obtained was led by the Swiss Thomas Keller with exactly 62,831,853,071,796 digits of Pi in 2021.

How to obtain it?

The value of Pi is obtained by dividing the length of a circumference by its diameter.

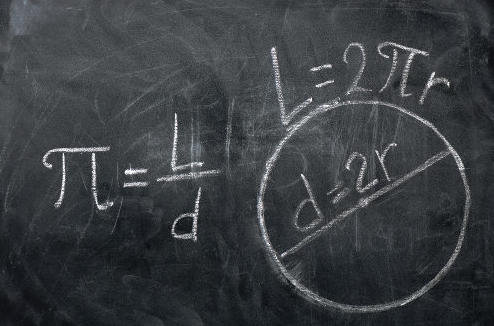
Some interesting facts…

• The Pi was studied for almost four thousand years by the human race. Around 2,000 B.C, the Babylonians established the constant rate of a circle as 3-1/8, also known as, 3.125. The Egyptians reached a slightly different value of Pi, of 3-1/7, also known as, 3.143;

• The symbol for Pi (π) has been used regularly in math only on the latest 250 years;

• On the episode of Star Trek (Wolf in the Fold), Spock kills the evil computer as he orders it to – compute what is the last digit of Pi;

• The sum of the first 144 digits of Pi equals 666 (it is what many scholars say that is the Number of the beast). And 144 = (6+6) x (6+6);

• In 1888 a doctor from Indiana – USA, Edward Johnson Goodwin, claimed to have succeeded in “framing” the circle. In his model he obtained π = 3.2. Ten years later, through the representative Taylor Record, he presented the project to the Indiana General Assembly claiming the value 16/5 as definitive truth. The project was unanimously approved by the House of Representatives in the Assembly;

Activity – “Weighing π”

Let’s approximate π by weighing a circle and a square!! How so? Let’s compare a circle with a radius of r and a square of side 2r. Observe the following figure:

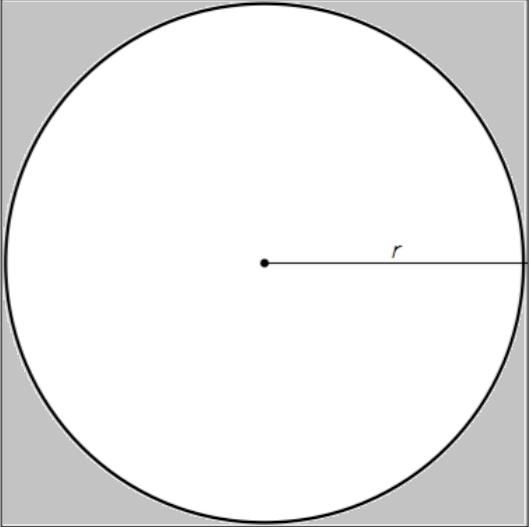
Now somehow obtain a circle and a square with the above proportions. One simple idea would be cutting many inscribed circles from square sheets, ideally many units. Another way would be to print in a 3d printer circle and squares (in this case, the pieces would have the same thickness and programmed so that the diameter of the circle would be equal as the side of the square). Lots of ideas could be given some thought, Ice shapes, sand boxes, etc. But how does it work?

Let’s weigh in the mass of the pieces:

M_\bigcirc=\sigma A_\bigcirc,\;\; M_\Box=\sigma A_\Box

In this case, consider σ as a constant that may as well be thought as the superficial density of the object and it must be the same for both objects (the physical meaning of this constant depends on the shape and how the experiment would come to be but, preferably, it is associated to the material and the width of the piece). The area of the circle and the square will be, respectively:

A_\bigcirc=\pi r^2,\;\; A_\Box=(2 r)^2.

The ratio of the masses will, therefore, be:

\dfrac{M_\bigcirc}{M_\Box}=\dfrac{\sigma A_\bigcirc}{\sigma A_\Box}=\dfrac{\cancel{\sigma}\pi \cancel{r^2}}{\cancel{\sigma} 4 \cancel{r^2}}=\dfrac{\pi}{4}.

Using the creativity, weight the mass, divide and multiply by 4 and, here we have an approximation for π.

As a tip for a school exercise it would be interesting to enjoy the experiment to talk about statistic, experimental errors etc. By using the sheets, for example, show the class how the approximation works better as the number of heavy sheets increases. To avoid the bad cuts made by the students when the mean is obtained is the median the better way out? Is it worth weighing all the units once?

Below there is a video with the experiments with the printed pieces.