Generalizing the Alcuin problem

Now that we’ve solved two versions of the same problem, it’s time for the moment mathematicians eagerly anticipate: generalization! But what is that?

Our first instinct might be to simply increase the number of characters, introduce complex conflict relationships, and then attempt to solve the same problem. In other words, given a set of characters, conflicts, and a boat, try to safely transport everyone to the other side of the river.

However, this kind of challenge, although potentially fun, can become as complicated as the conflict relationships we set up, especially when we have many characters and many relationships. It could become infeasible.

The most interesting questions now revolve around understanding what is common among the various versions of the same problem.

Questions like, given a set of characters and conflict relationships, what can we say about the minimum boat size that can safely carry everyone in multiple trips?

Note that answering this question doesn’t necessarily involve finding a way to transport the characters!

For instance, we can say that the total number of available seats on the boat must be less than or equal to the total number of characters. This is because a boat that can accommodate everyone can always transport the group in a single trip.

The idea now is to refine this estimate…

These are the kinds of questions that mathematicians generally like to answer.

Representing our problem better

Before we begin, let’s try to make things a little clearer.

In the previous problems (original problem, second problem), we represented conflict relationships between characters using a network. To do this, we replaced the characters with dots and represented the existence of a conflict between two characters with a line segment connecting the corresponding dots.

The images below show examples of some of these networks.

In mathematics, this kind of structure is known as a network or graph. The dots are called vertices, while the line segments are called edges.

Graphs are widely used in various areas of science and mathematics. They can be used to represent electrical circuits, computer networks, genealogical relationships, relationships between database entries, social network modeling, among thousands of other applications.

In this problem, our intention is to represent the conflicts existing between characters in Alcuin’s problem, and for that reason, we’ll use the term “conflict network” or “conflict graph“.

Great! Now that we have the object we want to study (the conflict network), we need to understand what we want to know.

We are interested in finding out the smallest boat with which we can solve Alcuin’s problem. In other words, the smallest boat with which we can transport everyone safely.

To simplify, let’s disregard the place of the ferryman. That is, when we say a boat has 3 seats, we mean the boat can accommodate the ferryman and 3 more characters.

The original problem, for instance, was represented by the following network, which we’ll call G:

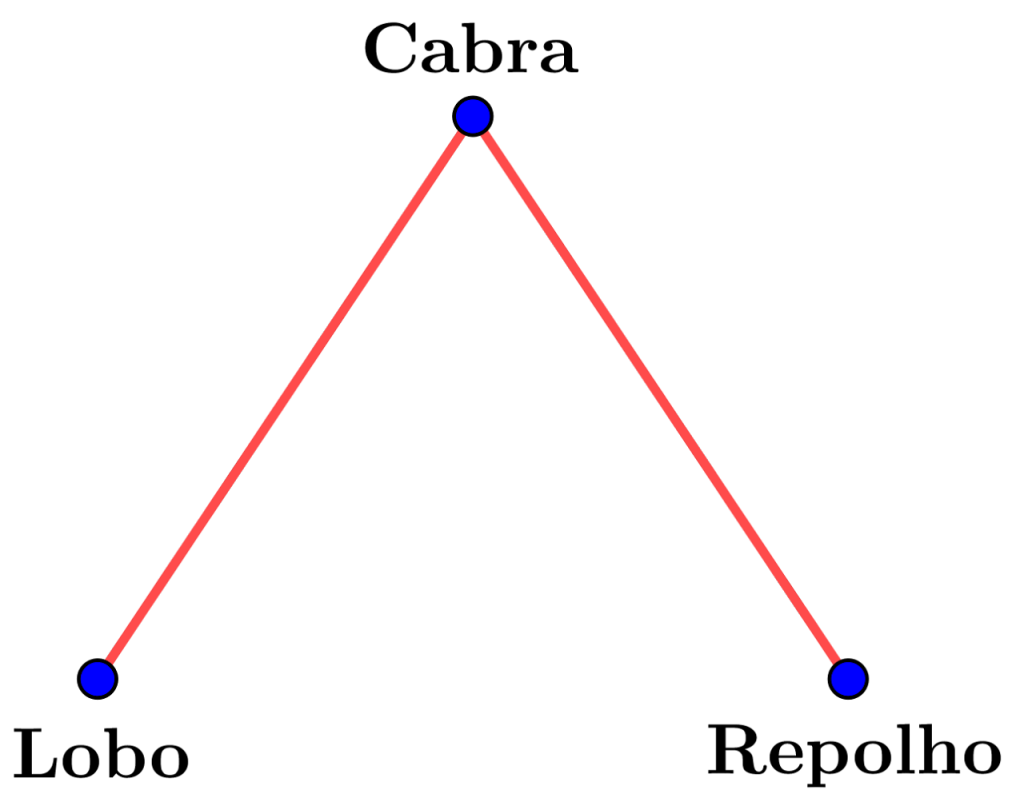
And the problem could be solved with a boat of just 1 seat. 

For this reason, we say that the Alcuin number of this network is 1, which can be summarized as al(G) = 1.

The second problem was represented by the network below (which we’ll call H):

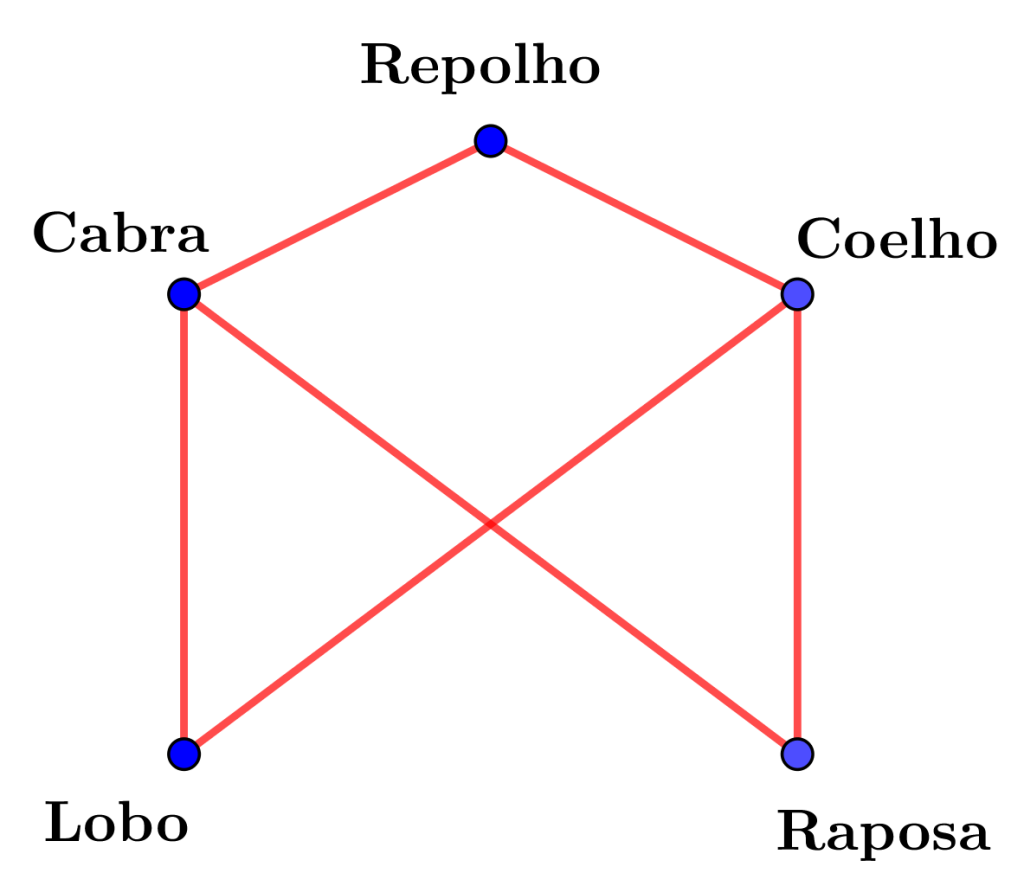
For this network, we saw that 1 seat on the boat was not enough, but with 2 seats, the problem had a solution.

Therefore, the Alcuin number of this network is 2. In other words, al(H) = 2.

In other words, given a conflict network R, we will call the Alcuin number the smallest number of seats on the boat for which the Alcuin problem in R has a solution, and we’ll denote this number as al(R).

Heading towards the solution…

So far, by representing characters and conflicts through a graph, we’ve narrowed down our problem to finding the so-called Alcuin number of the network. In other words, the smallest boat size with which we can transport everyone safely to the other side of the river.

Let’s start with a simple observation! Of course, if we can place all the characters in the boat, then all of them can be transported safely!

Translating the above observation into a conflict network G, we have the following expression:

al(G) ≤ number of vertices in G

But we can do better than that!

To do this, let’s go back to the last problem we analyzed. In that case, we worked with the network in the image above and determined that al(G) = 2.

But why couldn’t we solve the problem with a single-seat boat? Do you remember?

If you don’t remember, take a moment to think more about the problem before continuing! The answer lies in the very first crossing we make with the boat. Ask yourself: what should happen to the network when we remove characters from the group and put them in the boat? What can we achieve by removing 2 characters that we can’t achieve with just 1?

Remember now?

What we need is for there to be no conflicts between the characters left alone on the bank. Looking at network G, we need to remove two vertices in such a way that there is no edge connecting the remaining vertices!

See below what happens to the previous network when we remove the Goat and the Rabbit!

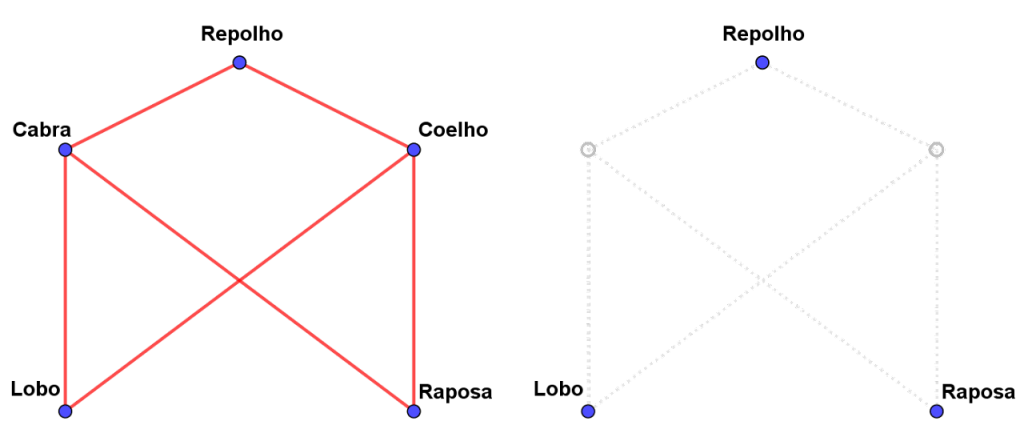
A set of vertices with this property is known as a cover of the network.

Thus, to determine the boat size, we need to find a cover of the conflict network. And if we want the smallest possible boat, we need to know the size of the smallest possible cover of the network.

In mathematics, we have a fancy name for the number of vertices in the smallest cover of a network, which we call the minimum vertex cover number of the network.

To help you understand this concept a bit better, play around with the app below. Remove vertices from the network to try to find the smallest cover of the graph. When you’re ready, press the button to show a possible minimal cover and discover the minimum vertex cover number of the network.

Great! With this, we see that the boat that solves the problem must have space to accommodate at least a minimum cover of the conflict network. In other words,

al(G) ≥ minimum vertex cover number of G

But is that always enough? Can we always transport all the passengers safely using a boat with a size exactly equal to that of the minimum cover?

To understand this problem, consider the following network:

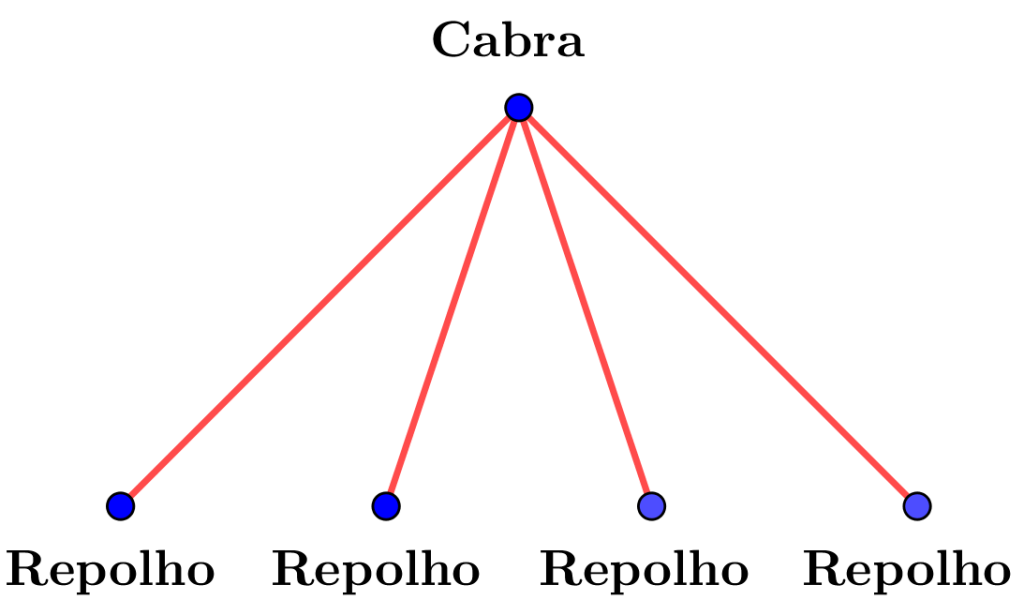
Before continuing, take a moment to think about the above network…

What is the minimum vertex cover number of the network?

It shouldn’t be hard to see that by removing the Goat, all edges disappear! Thus, the minimum vertex cover number of this network is 1!

But can we transport all the passengers using a boat with only one seat?

Try to think about this… Take a pen and paper and draw out the problem. See if you can solve it.

After a few attempts, you should realize that it’s simply not possible to solve the problem represented by the network above with a boat of just 1 seat!

This shows us that there are networks for which the Alcuin number is strictly greater than the minimum vertex cover number!

But how much greater does it need to be?

Go back to the network in the figure above and try to answer this question. Can you solve the transportation problem with a boat of 2 seats?