Beats

Harmonic oscillations
Harmonic Oscillations are processes characterized by some form of repetition, as seen in the swaying of a pendulum, for instance. The simplest oscillations that manifest in nature are termed harmonic oscillations. These are oscillations in which the varying quantity, such as the deflection angle of a pendulum, changes with time according to either the sine or cosine function (in the case of a pendulum, particularly when the amplitude is small).

They hold importance for two principal reasons:

• Natural oscillations often closely mimic harmonic oscillations;
• More intricate oscillatory phenomena can be described as the superposition of numerous harmonic oscillators.

Mathematical representation:

A harmonic oscillator can be mathematically described by the real function:

x (t) = A \cos (\omega t + \alpha),

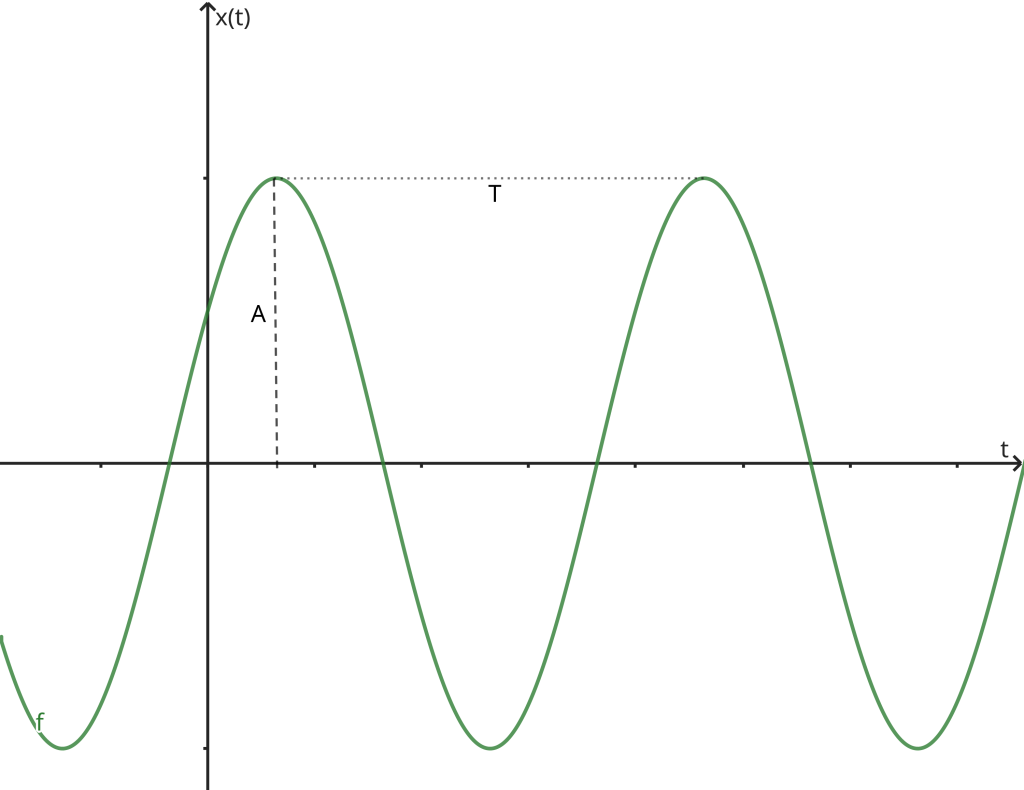
Since the cosine function is confined between +1 and -1, the values of x vary between +A and -A. The positive quantity A represents the maximum conceivable variation of the oscillation with respect to its equilibrium value, referred to as amplitude. The argument of the cosine, ωt + α, is referred to as the oscillation’s phase.

Given that the cosine function is periodic with a period of 2π, distinct positions x of the oscillator will repeat within the time interval T, during which the phase accumulates an increment of 2π. This interval T is identified as the oscillation period, yielding the condition

x (t + T ) = x (t) \Leftrightarrow (t + T ) + \alpha =t+ \omega t + \alpha + 2\pi\Leftrightarrow T =\frac{2\pi}{\omega}

The oscillation frequency ν is defined as the number of oscillations per unit of time, i.e., ν = 1/T. Thus, ω = 2π/T represents the number of oscillations in 2π units of time, also known as angular frequency.

Beat Phenomenon

A special scenario emerges when two harmonic oscillators x1(t) and x2(t) are combined with nearly proximate frequencies. The resultant motion can be regarded as that of a solitary harmonic oscillator with pulsating amplitude. Such oscillations are termed beats.

Let ω denote the angular frequency of oscillator x1, and let ω + δω denote the angular frequency of oscillator x2. Their summation is expressed as:

x(t) = x_1(t) + x_2(t) = A \cos(\omega t) + A \cos((\omega + \delta\omega) t),

For the sake of simplicity, we adopt the initial phase as zero for both oscillators. Utilizing the trigonometric identity:

\cos(a) + \cos(b) = 2 \cos\left(\frac{a+b}{2}\right) \cos\left(\frac{a-b}{2}\right),

we obtain:

x(t) = 2A \cos\left(\frac{\delta\omega}{2} t\right) \cos(\omega t + \phi),

where \phi = \frac{\delta\omega}{2}t denotes the initial phase of the beat. Assuming ω to be substantially greater than \delta\omega, \omega \gg \delta\omega, we deduce:

x(t) = 2A \cos\left(\frac{\delta\omega}{2}t\right) \cos(\omega t).

whose graphical representation can be depicted as:

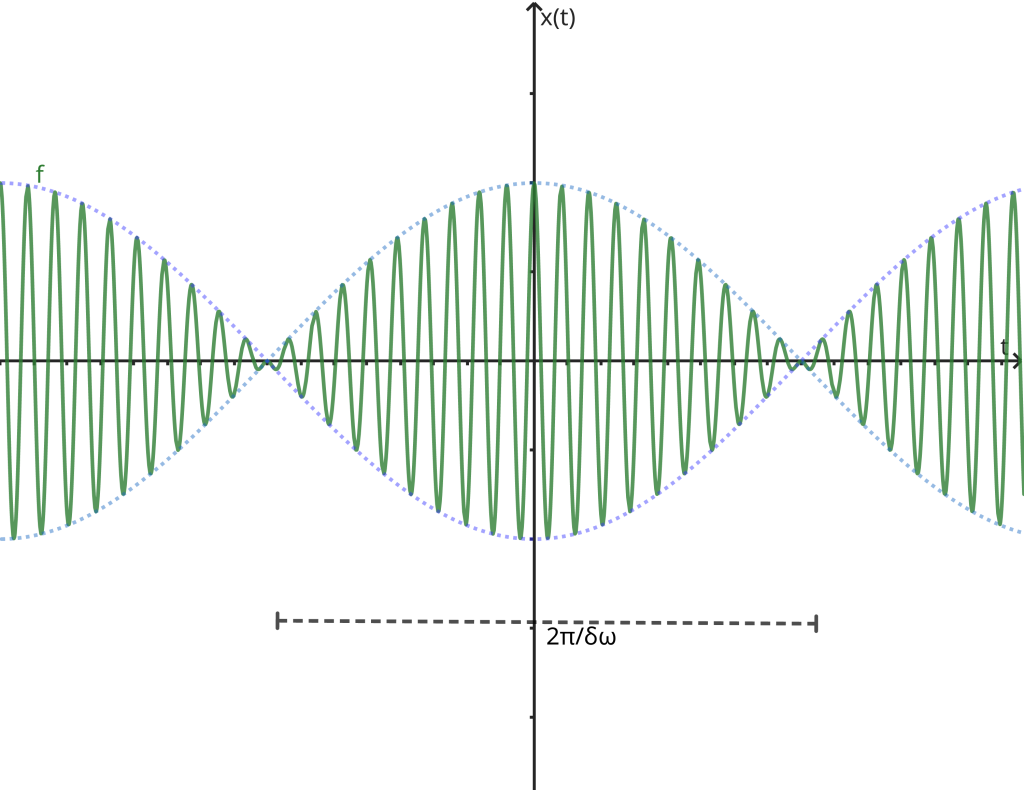
n the illustration, we observe that owing to the condition \omega \gg \delta\omega, o termo \cos(\omega t) he term cos(ωt) completes several full oscillations, while the factor 2A\cos(\frac{\delta\omega}{2}t) remains virtually unchanged. Consequently, we can interpret x(t) as a harmonic oscillator of frequency ω, the amplitude of which varies in accordance with a periodic law. The amplitude of oscillation is inherently positive, hence:

Amplitude = |2A \cos(\frac{\delta\omega}{2}t)|.

The angular frequency of amplitude oscillation is twice the oscillation frequency
of the factor 2A \cos(\frac{\delta\omega}{2}t). Specifically, the angular frequency of amplitude corresponds to \delta\omega, equal to the diference between those of oscillators x_1 e x_2. Thus, the beat period is determined as T=\frac{2\pi}{\delta\omega}.

Application

The beat phenomenon is commonly harnessed by musicians for instrument tuning through the use of a tuning fork,

OThe tuning fork is calibrated to oscillate
at a specific frequency (A4 at 440 Hz). By bringing it close to a vibrating string with a frequency slightly distinct from that of the tuning fork (the string requiring tuning), pronounced beats ensue, as elucidated above. By adjusting the string’s tension to synchronize its vibration frequency with the oscillation frequency of the tuning fork, the frequency difference δω tends towards zero, causing the beats to diminish. At this juncture, the string is considered to be tuned.

Shall we conduct an experiment?

Below, you can select the frequencies of two generated waves, observe the resulting graph (the oscillation count on the graph is reduced for enhanced visualization), and even listen to the resulting sound wave—the beat!

As an exercise, endeavor to calculate the period based on the chosen numerical values. In the example provided below, we have: T=|\frac{1}{\nu_1-\nu_2}|.