Disco de Poincaré e Geometria Hiperbólica

Histórico

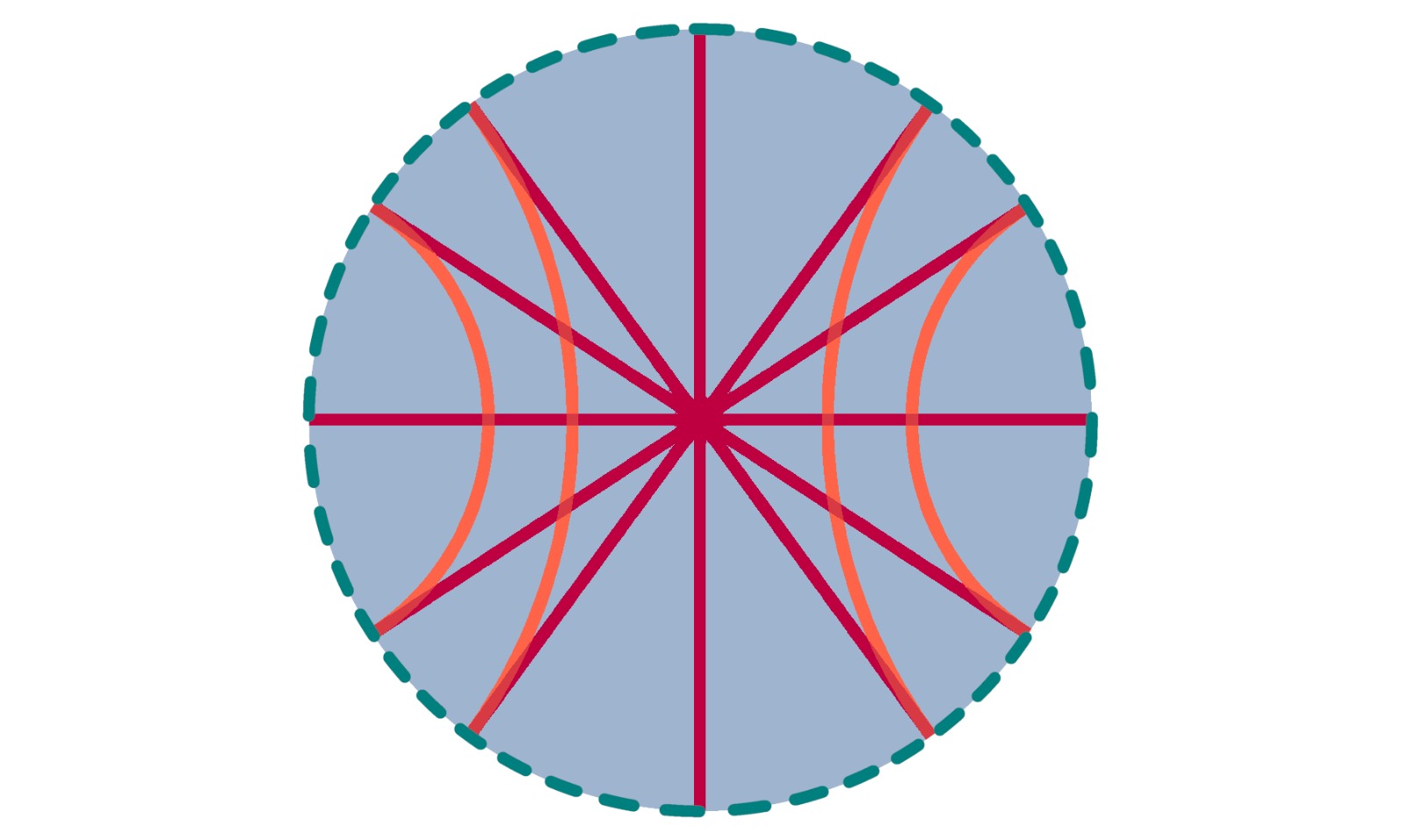
O Disco de Poincaré é uma representação visual da geometria hiperbólica desenvolvida pelo matemático francês Henri Poincaré no final do século XIX. A motivação por trás dessa representação surgiu da busca de entender e explorar geometrias não euclidianas, que eram uma quebra de paradigma em relação à geometria clássica de Euclides.

Essa atividade foi planejada com o intuito de introduzir o leitor à geometria não euclidiana por meio de uma abordagem visual e interativa. Nosso objetivo é auxiliar o leitor a compreender as propriedades singulares da geometria hiperbólica, utilizando o Disco de Poincaré como uma ferramenta de visualização. A geometria hiperbólica emerge de um axioma onde, dados um ponto e uma reta nesse espaço, existem mais de uma (infinitas) retas que passam por esse ponto e não se intersectam com a reta fornecida.

O Disco de Poincaré desempenhou um papel fundamental na compreensão das geometrias não euclidianas proporcionando uma representação visual para a geometria hiperbólica. O modelo de disco, originalmente proposto por Bernhard Riemann durante uma palestra em 1854 (que foi posteriormente publicada em 1868), ganhou mais destaque por meio de um artigo de Eugenio Beltrami no mesmo ano. No entanto, foi Henri Poincaré quem incorporou o modelo em um tratamento abrangente de funções hiperbólicas, parabólicas e elípticas em seu trabalho de 1882. O reconhecimento do modelo, no entanto, ocorreu com a obra filosófica de Poincaré em 1905, “Ciência e Hipótese”, na qual ele introduziu um universo conceitual agora conhecido como o disco de Poincaré. Dentro dessa região, o espaço é descrito por elementos euclidianos, porém de maneira intrigante, para os habitantes deste disco a geometria é hiperbólica, apresentando uma fascinante ligação entre as duas geometrias.

Descrição da atividade

Listamos abaixo as atividades onde inicialmente propomos uma intuição sobre como as distâncias comportam-se de maneira distinta para habitantes do disco. Posteriormente propomos a construção da disco de Poincaré.

Caminhantes no disco de Poincaré

Considere habitantes que vivem dentro de uma área delimitada por uma circunferência. Algo muito particular ocorre com eles, suas pernas encolhem continuamente à medida que se afastam do centro da circunferência. De modo mais específico, considere que a circunferência tenha raio R e que quando a perna encontra-se a uma distância r do centro da circunferência, a perna do caminhante terá comprimento proporcional a R²-r² de seu valor no centro. Para os caminhantes, as distâncias dentro deste disco são contadas a partir da quantidade de passos que eles necessitam para se deslocar de um ponto a outro.

Desafios:

1. Dados 2 pontos no interior deste disco, como são os caminhos nos quais os caminhantes realizam menos passos entre os pontos? Ou seja, como são os caminhos de menor comprimento?

2. Considere que um caminhante tenha um passo de tamanho \frac{1}{2} quando ele inicia seu passeio no centro do disco com raio R=1. Com quantos passos ele chegará na fronteira delimitada pela circunferência? Seria possível para um caminhante do disco ultrapassar a fronteira?

Dica: a distância euclidiana r_n do centro ao n -ésimo passo é dada por r_n= \frac{3^n-1}{3^n+1}.

A dica acima utiliza o fato de que se r é a distância euclidiana entre o centro e um ponto no disco, então a distância para os habitantes no disco é dada por ln(\frac{1+r}{1-r}), que deve ser posteriormente reescalada para o tamanho dos passos.

Construção do disco de Poincaré (Faça em casa/escola)

Podemos construir o disco de Poincaré ao descrever o comportamento das retas no espaço. Como visto na atividade dos caminhantes no disco, a distância do centro até a fronteira será infinita para os habitantes deste espaço. Porém, as retas são definidas pelos menores caminhos no disco e, de maneira simplificada, veremos a seguir como construir os menores caminhos nesta geometria.

Resumidamente, os menores caminhos serão retas que intersectam o centro da circunferência e círculos ortogonais, isto é, arcos que pertences a circunferências cujas tangentes intersectam perpendicularmente a fronteira (tangentes) do disco. Os menores caminhos são denominados geodésicas.

Antes de iniciarmos a construção, relembremos como definimos a inversão de pontos por uma circunferência.

Inversão de pontos

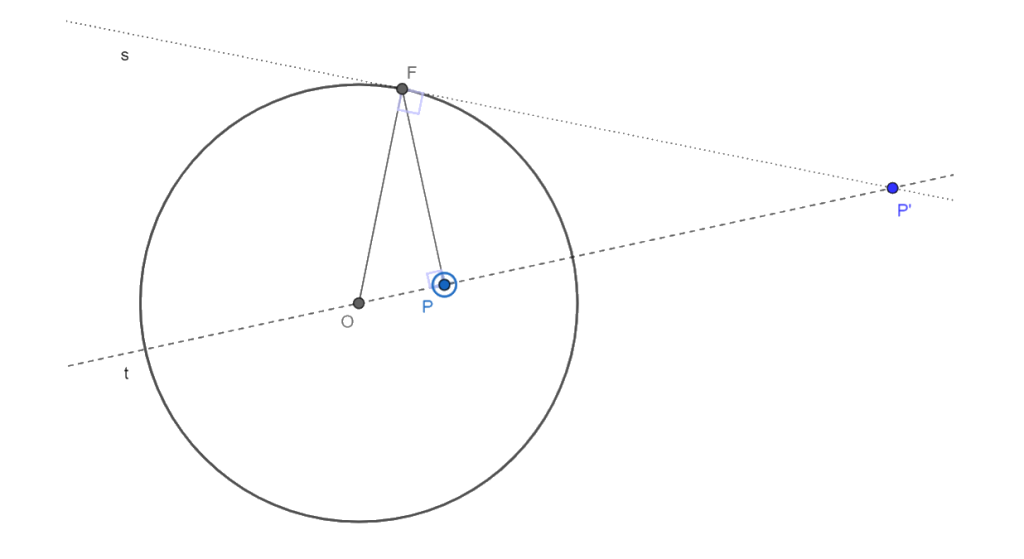
• Seja P um ponto no interior de uma circunferência com centro O e defina t sendo a reta que contém O e P
• Considere F um ponto da circunferência que pertença à reta perpendicular a t que intersecta o ponto P
• Seja s a reta perpendicular ao segmento OF
• O ponto P’ é a inversão de P pela circunferência quando P’ é o ponto de intersecção entre as retas s e t

Caminhos no disco de Poincaré

Considere P e Q pontos no interior do disco. Seja l a reta determinada por P e Q. Se O pertence a l, então o menor caminho entre P e Q é o segmento de reta PQ. 

Caso contrário realizamos a seguinte construção com régua e compasso:

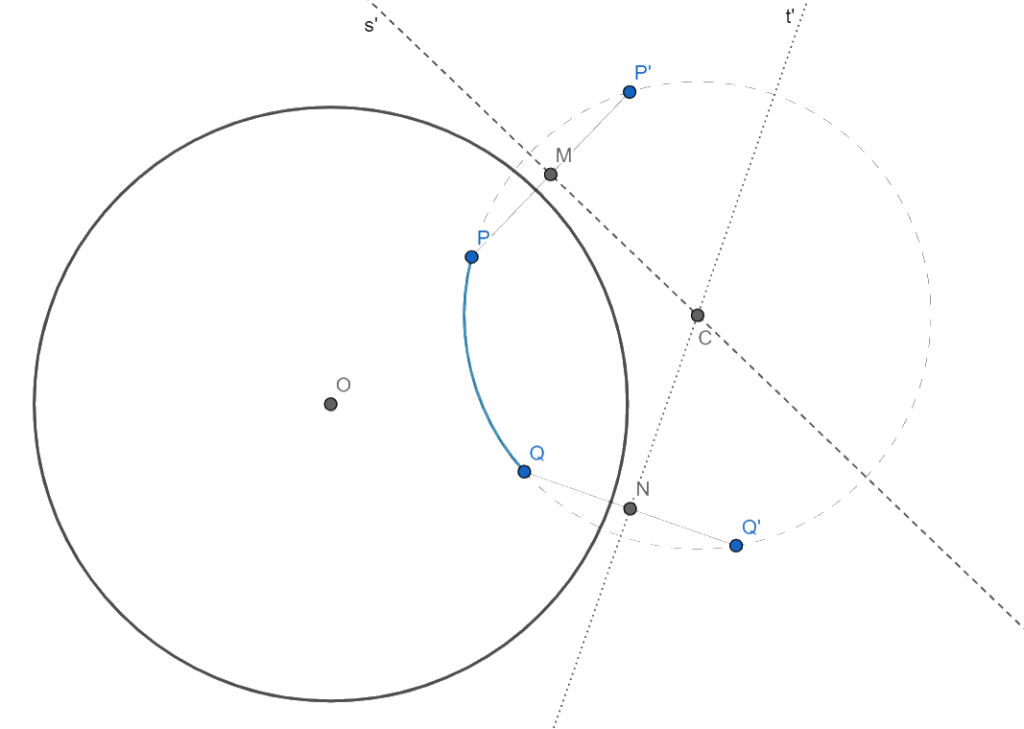
• Sejam P’ e Q’ a inversão de P e Q pelo disco
• Considere M e N os pontos médios de PP’ e QQ’, respectivamente
• Sejam s’ e t’ as retas perpendiculares a PP’ e QQ’
• Defina C sendo o ponto de intersecção entre s’ e t’
• O arco de circunferência entre P e Q com centro em C é a geodésica entre P e Q no disco de Poincaré

Propriedades do Disco

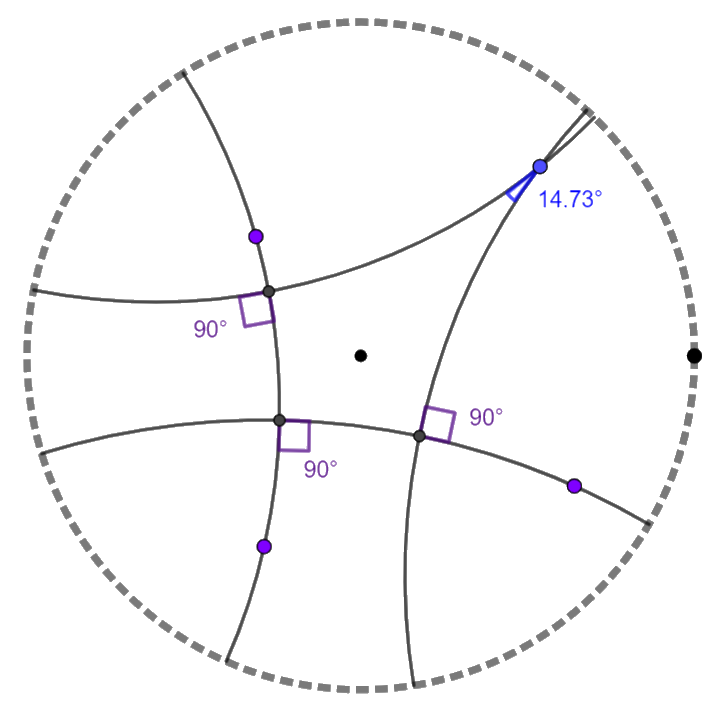
Este disco nos permite verificar diversas propriedades das geometrias hiperbólicas. Por exemplo, podemos construir um quadrilátero de Khayyam-Saccheri. Apesar deste quadrilátero possuir três ângulos retos, o quarto ângulo interno será agudo. Consequentemente, a soma dos ângulos internos será menor que 2\pi.

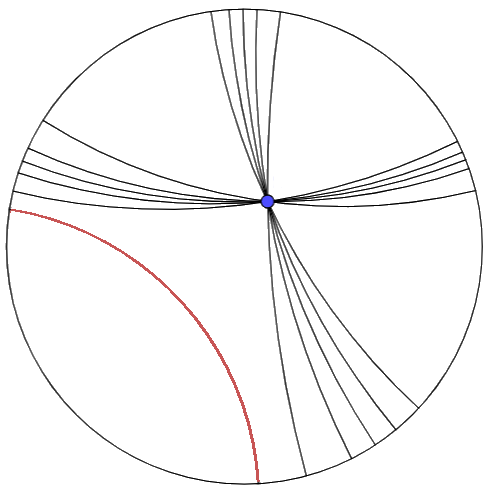
Como a geometria não euclidiana baseia-se em desconsiderar o postulado das paralelas, temos como evidência a existência de múltiplas retas paralelas entre uma reta e um ponto.

Saiba mais

Explore mais as propriedades da geometria hiperbólica no disco de Poincaré na seguinte aplicação https://www.geogebra.org/m/mpzwcqka (disponibilizada por Guilherme A. Rink)

Uma outra opção seria a usar uma aplicação mais construtiva como a disponível em https://www.geogebra.org/m/R5e9AggU (em inglês)

No vídeo a seguir podemos ver uma representação do disco com carros que vivem neste espaço (em vez de caminhantes) assim uma associação com uma propriedade projetiva entre uma superfície eo disco https://youtu.be/nu4mkwBEB0Y?feature=shared 

Este modelo também foi explorado nas artes, de modo especial por Escher em algumas obras, veja https://mathstat.slu.edu/escher/index.php/Circle_Limit_Exploration
Caso tenha interesse em saber mais sobre a teoria por trás do disco de Poincaré com matemática avançada (nível superior), recomendamos o texto “Poincaré and his disk” por Étienne Ghys (em inglês) https://perso.ens-lyon.fr/ghys/articles/Poincarediskenglish.pdf