O problema das três cartas (Solução)

Vamos enumerar as cartas e faces da seguinte maneira:

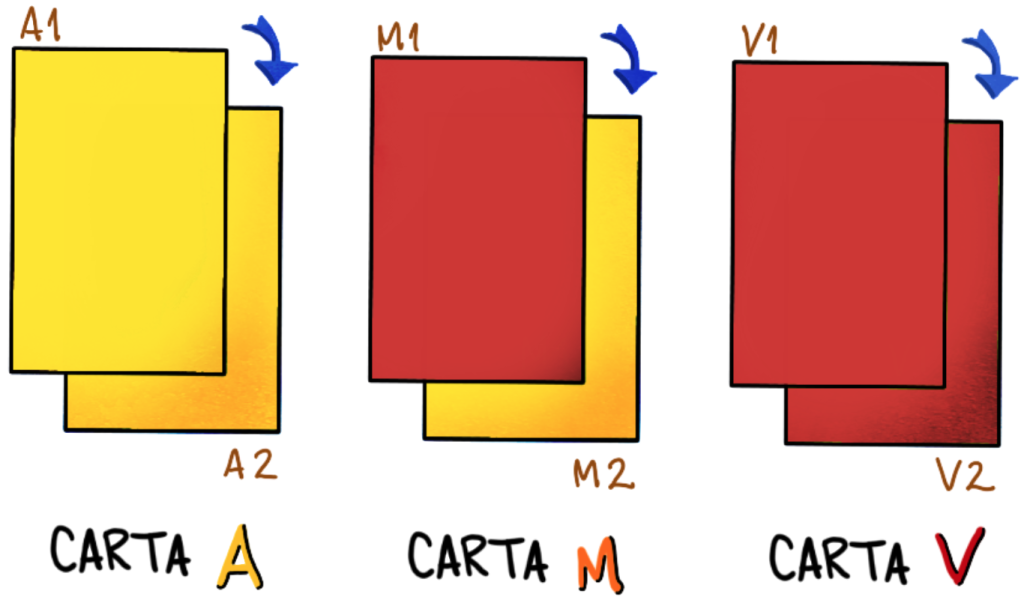
• Carta A (amarela)    com faces: Amarela   (A1) – Amarela   (A2) 
• Carta M (misturada) com faces: Vermelha (M1) – Amarela  (M2)
• Carta V (vermelha)   com faces: Vermelha (V1) – Vermelha (V2)

Nesse contexto, considere como carta C qualquer uma, ou seja, uma das cartas A, M ou V. Assumimos que (Ci,Cj) representa o(a) jogador(a) vendo a face Ci mantendo a face Cj oculta; se fosse a mesma carta mas o jogador visse a face Cj, chamamos de (Cj,Ci).

Com isso, todas as combinações possíveis são dadas pelo seguinte conjunto:

{(A1,A2), (A2,A1), (M1,M2), (M2,M1), (V1,V2), (V2,V1)}.

Agora, supondo que o jogador está vendo uma face amarela, temos que o espaço de eventos possíveis (nesse caso, podemos explicar um pouco sobre Probabilidade Condicional) seria o Espaço Amostral total sem as faces da carta totalmente vermelha, ou seja:

{(A1,A2), (A2,A1), (M2,M1)}

Claramente, teremos duas situações com a face escondida amarela e uma com a face escondida vermelha. Como não há qualquer peso no sorteio, ou seja, os eventos são equiprováveis, a chance de a face oculta ser vermelha, dado que a face exibida é amarela, se reduz a ⅓.

Comparação com o problema de Monty Hall

A explicação acima é direta e clara, porém o fato de o resultado apresentar probabilidades semelhantes ao problema de Monty Hall, podendo ser contraintuitivo, nos possibilita compará-los lado a lado.

Considere que teremos 3 portas A, M e V que representam cada carta com o mesmo nome. O lado visível da carta é equivalente ao apresentador abrir a porta com duas cores distintas da cor revelada (a porta sem o prêmio). Com isso, a única escolha de porta permitida antes da revelação seria a porta M (com duas cores diferentes). Deste modo, trocar de porta é equivalente a escolher a carta com os dois lados com a mesma cor revelada!

Note que, neste caso, a escolha inicial da porta M é de fato obrigatória, o que não altera a probabilidade de ⅓ de ser a carta retirada.