 Na imagem visualizamos o logotipo do projeto 'MatematiZou', escrito com letras de forma na cor verde-azulada. A letra “Z” está na cor branca dentro de um hexágono com pontas arredondadas preenchido na mesma tonalidade de cor do restante das letras.  Na imagem temos um mini caminhão branco de madeira, cuja caçamba é azul escura e está escrito em letras brancas “UFABC”. As rodas do caminhão são vermelhas e quadradas. Cada par de rodas do caminhão está em cima de uma pista com ondulações.  Na imagem, há várias pessoas participando do evento “UFABC para todos” no Ginásio da UFABC campus Santo André. Algumas pessoas estão ao redor de uma mesa com jogos que incluem copos, mapas, tabuleiro de xadrez, entre outros, e outras, estão vendo as exposições espalhadas por todo o ambiente.](https://matematizou.gradmat.ufabc.edu.br/files/LogoMatematizouTeal.png)
Desafio 1. Dados 2 pontos no interior deste disco, como são os caminhos nos quais os caminhantes realizam menos passos entre os pontos? Ou seja, como são os caminhos de menor comprimento?
Resposta:
O objetivo deste desafio é descrever qualitativamente como serão os menores caminhos (geodésicas) dos habitantes do disco.
Diferentemente do plano euclidiano, não podemos considerar que um segmento de reta será a menor distância entre os pontos. Note que quando os caminhantes andam em direção ao centro do disco suas pernas são maiores, logo os passos são mais largos. Portanto, podemos afirmar que os caminhos que tendem ao centro são menores, gerando uma curva direcionada ao centro. De fato, tal comportamento é observável (veja a imagem abaixo).
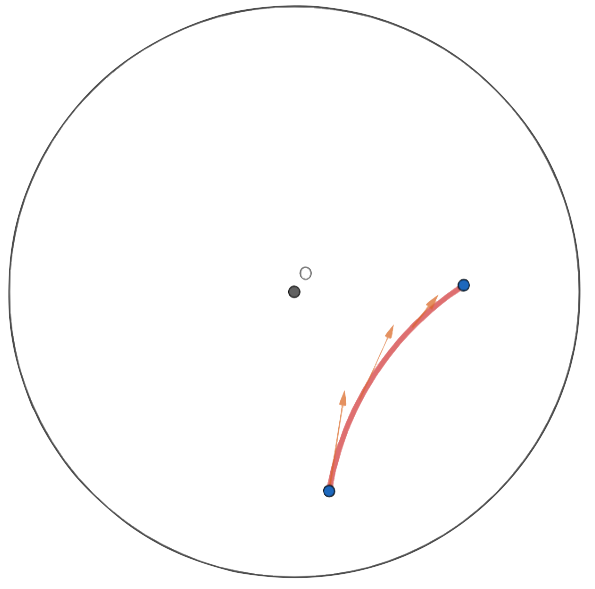
Não é escopo desta atividade mostrar quais serão os caminhos nesse espaço. Porém, afirmamos que eles se dividem em dois: caso a linha reta determinada pelos dois pontos intersectar o centro, então o segmento de reta será a geodésica. Quando isso não ocorre, ele será um arco de uma circunferência ortogonal ao disco. Veja na seção “Construção do disco de Poincaré” como podemos obter tais caminhos.
Desafio 2: Considere que um caminhante tenha um passo de tamanho 1/2 quando ele inicia seu passo no centro do disco de raio R=1. Com quantos passos ele chegará na fronteira delimitada pela circunferência? Seria possível para um caminhante do disco ultrapassar a fronteira?
Dica: a distância euclidiana r_n do centro ao n-ésimo passo é dada por r_n= \frac{3^n-1}{3^n+1}.
* A dica acima utiliza o fato de que se r é a distância euclidiana entre o centro e um ponto no disco, então a distância para os habitantes no disco é dada por ln(\frac{1+r}{1-r}), que deve ser posteriormente reescalada para o tamanho dos passos. Com isso, cada passo possui comprimento ln(3) dentro do disco (ou seja, para seus habitantes), o que corresponde para nós, observadores externos, em um comprimento 1/2 do raio euclidiano no primeiro passo do caminhante.
Resposta:
Usaremos a dica para resolução do problema. O caminhante atingirá a fronteira no n-ésimo passo quando r_{n-1}<1 e r_n\geq 1 (considerando que o n-ésimo passo pode ser menor que um passo completo).
Portanto, buscamos n tal que r_n= \frac{3^n-1}{3^n+1} \geq 1. Contudo, ao supormos que essa afirmação seja verdadeira, teríamos 3^n-1 \geq 3^n+1, ou seja, que -1 \geq 1, o que é um absurdo. Portanto, o caminhante nunca chega até a fronteira em tempo finito. Em outras palavras, o segmento entre o centro do disco e a fronteira é infinito.
A resposta acima também garante que o caminhante não ultrapassa a fronteira. Porém, suponha adicionalmente que este indivíduo já esteja na fronteira. Então o comprimento de suas pernas é zero, pois segue a proporção de 1^2-1^2=0. Portanto, a resposta é sempre negativa para este item.
Um fato curioso é que este problema pode ser comparado com o paradoxo de Zenão. Contudo, neste caso a geometria é diferente fazendo o espaço dilatar-se pelo ponto de vista dos habitantes do disco, o problema é modificado considerando a quantidade de passos em vez do próprio espaço em si.
