Topologia Visual

Motivação

O principal objetivo desta atividade é apresentar ao público experimentos matemáticos usando ferramentas visuais (ver [3]). Nosso experimento topológico básico ajudará o público a redescobrir instigantes propriedades matemáticas. Esse experimento é baseado em objetos topológicos bem conhecidos tais como: faixa de Möbius e a garrafa de Klein.

Nesta exposição, mostramos a beleza da topologia para um público geral utilizando uma terminologia simples. Mesmo que os resultados não sejam intuitivos, o público pode se fazer muitas perguntas interessantes.

Faixa de Möbius

Uma faixa de Möbius (ou banda de Möbius) é uma superfície com uma meia volta que
tem exatamente um bordo e exatamente uma face.

Para construir uma faixa de Möbius, começamos pegando uma longa faixa retangular
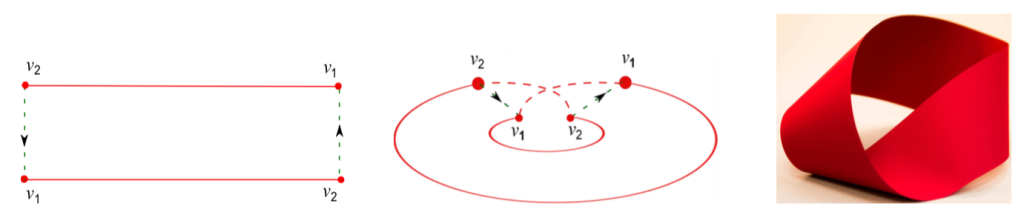
de papel e rotulando as extremidades de suas arestas com v_1 e v_2 de modo que não haja duas extremidades consecutivas com o mesmo rótulo (ver Figura 1(a)). Observe que as setas na Figura 1(a) vão de v_2 a v_1 (onde v_1 é a cabeça e v_2 a cauda das setas); isso nos indica como os extremos da faixa retangular devem ser colados na próxima etapa. A faixa de Möbius é obtida colando as bordas curtas desse retângulo, ou seja, identificando ponta com ponta (v_1 com v_1) e rabo com rabo (v_2 com v_2) das setas. As duas extremidades
rotuladas com v_1 irão se sobrepor e, da mesma forma, as extremidades rotuladas como v_2 irão se sobrepor na etapa final, conforme visto na Figura 1(b). Além disso, devemos ter em mente que as linhas tracejadas vistas na Figura 1(b) são virtuais; nós as mostramos para indicar que as duas cabeças das setas marcadas com v_1 são, na verdade, as mesmas. Da mesma forma, as duas caudas rotuladas como v_2 são as mesmas.

Questão 1: Passe os dedos ao longo da borda a partir de um ponto fixado (certifique-se de que está na borda).

• É possível retornar ao ponto fixado sem levantar os dedos nem uma vez?
• Qual é o número total de bordas que a faixa pode ter?

Questão 2: Segure a faixa de Möbius entre dois dedos a meio caminho da borda (indicador em cima e polegar embaixo). Marque um ponto Q_1 ao lado de um dedo e Q_2 ao lado do outro dedo (ver Figura).

• É possível mover um dedo de Q_1 para Q_2 através do centro da faixa sem levantar o dedo nem uma vez?
• Quantas faces existem na faixa de Möbius?

Cortando a Faixa de Möbius

Corte a faixa de Möbius ao longo da sua linha média (conforme descrito na figura).

• Quantas torções resultarão após o corte?
• Quantas faixas resultarão após o corte?
• Quantas faces resultarão após o corte?
  

Cortando novamente a Faixa de Möbius

Corte a faixa resultante do experimento anterior novamente ao meio.

• Quantas torções resultarão após o corte?
• Quantas faixas resultarão após o corte?
• Quantas faces resultarão após o corte?

Referência

1. S. Barr, Experiments in Topology, Reprint of the 1964 original. Dover Publications,
   Inc., Mineola, NY, 1989.
2. D. Davis, Algebraic Topology -There’s an App for That, Math Horizons, September
   2011.
3. R. Flórez and A. Mukherjee, Classroom experiences in introducing students to conjectures, exploration and visual proofs using experiments on the mobius strip. PRIMUS. 30.1 50-66, 2020. A version in PRIMUS.
4. J. Tanton, A dozen questions about a donut, Math Horizons, November 1998.