Projeção Estereográfica

Fixado um ponto X de uma esfera, a projeção estereográfica consiste em projetar, a partir de X, toda a esfera sobre um plano, de modo que o ponto X corresponda ao infinito do plano de projeção. Usualmente, toma-se o polo norte da esfera, denotado por N, como sendo o ponto fixado. Neste caso, para cada ponto P da esfera, diferente do polo norte N, a imagem de P pela projeção estereográfica, denotada por P', é o ponto de intersecção da semirreta \overrightarrow{NP} com o plano de projeção escolhido. Quando se considera a projeção estereográfica em relação ao polo norte, são geralmente tomadas as duas seguintes escolhas para o plano de projeção:

1. O plano de projeção tangencia a esfera em seu polo sul, denotado por S, como está ilustrado na Figura 1.

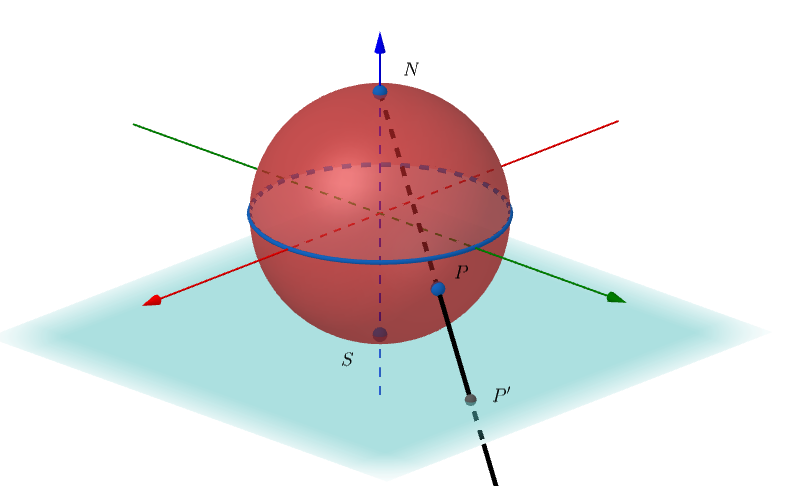
Você consegue imaginar qual será a imagem do equador da esfera pela projeção estereográfica? Pense alguns instantes, antes de visualizar a próxima imagem.

Quando o plano de projeção tangencia a esfera no polo Sul, a imagem do equador da esfera pela projeção estereográfica é também uma circunferência \mathcal{C} que está contida no plano de projeção e cujo centro é o ponto S, como está ilustrado na Figura 2. Note que, deste modo, o hemisfério norte da esfera será projetado sobre o exterior de \mathcal{C} no plano de projeção, enquanto que o hemisfério sul sobre o interior de \mathcal{C} no plano de projeção.

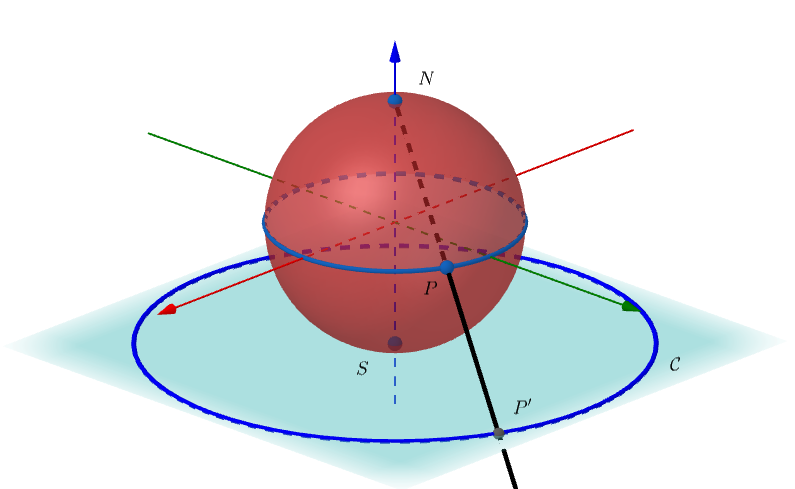
2. O plano de projeção contém o equador da esfera, como está ilustrado na Figura 3.

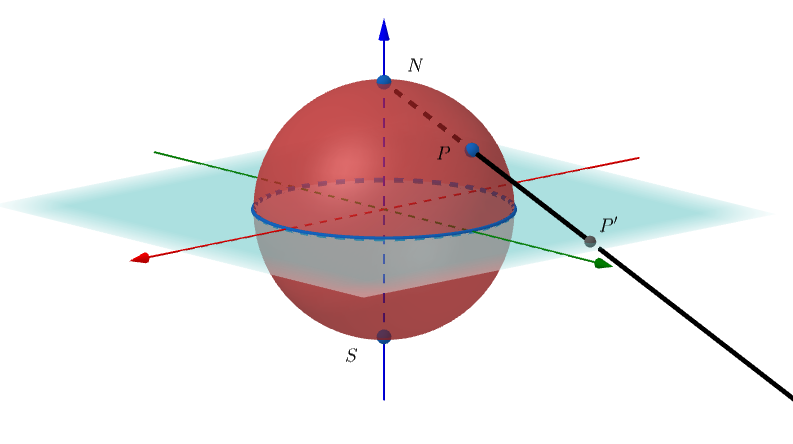
Neste caso, o equador da esfera permanece fixado pela projeção estereográfica. O hemisfério norte é levado pela projeção estereográfica sobre o exterior do equador da esfera no plano de projeção, enquanto que o hemisfério sul é levado sobre o interior. Para qual ponto é levado o polo sul?

Aplicações

Uma aplicação bem conhecida da projeção estereográfica é na Cartografia Náutica. Neste caso, o plano de projeção é tangente à superfície terrestre num dos polos (como no Caso 1 anterior), de modo que a representação plana de uma região polar pode ser obtida sem muitas distorções. Pense um momento na seguinte situação: considerando a projeção estereográfica a partir do polo norte sobre o plano que tangencia a Terra no polo sul, como ficarão os paralelos e meridianos da Terra na projeção?

A Figura 4 ilustra bem esta situação.

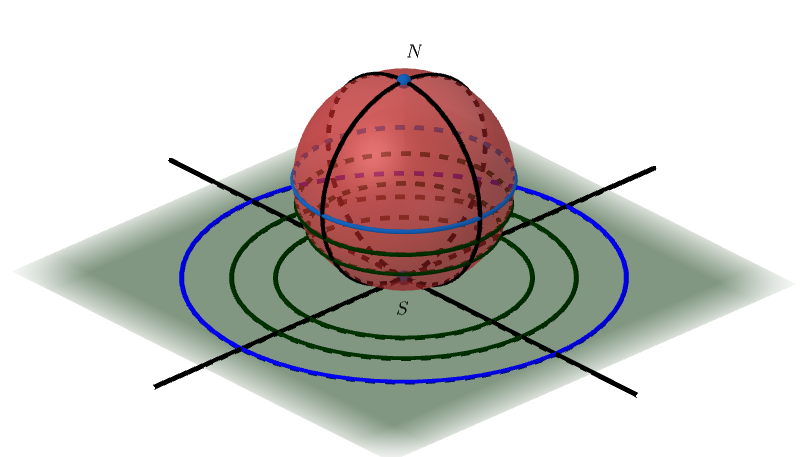
Imagine como seria o mapa geográfico da Terra se fosse utilizada a projeção estereográfica. Você verá o mapa do hemisfério norte obtido por meio da projeção estereográfica a partir do polo sul sobre o plano que tangencia a Terra no polo norte acessando o link \url{https://encurtador.com.br/kxJPU}

Uma outra aplicação que vem sendo adotada nos últimos anos é a produção de fotografias utilizando projeção estereográfica. Muitas delas podem ser encontradas e visualizadas na rede, como as que estão acessadas pelos links \url{https://encurtador.com.br/kDF37} e \url{https://encurtador.com.br/ckpuw}

Como fazer em casa/na escola?

Uma possível atividade sobre projeção estereográfica que pode ser realizada em casa ou na escola utiliza somente uma bola (oca) de isopor, uma folha de papel, um palito de churrasco e um lápis. Apoia-se o papel sobre uma mesa e sobre o papel apoia-se a bola de isopor, de modo que ambos não deslizem. Sobre a bola de isopor, marcam-se alguns pontos, diferentes do polo norte da bola. Em seguida, a partir do polo norte, passa-se o palito de churrasco furando a bola de isopor nos pontos escolhidos. Com o lápis, marcam-se os pontos em que o palito toca o papel. Os pontos marcados sobre a folha de papel são as imagens pela projeção estereográfica dos pontos marcados sobre a bola de isopor.

Saiba mais

Para saber um pouco mais sobre a projeção estereográfica, acesse as seguintes referências:

• Gazeta de Matemática. Disponível em https://gazeta.spm.pt/get?gid=168 Acessado em: 21/08/2023.

• José M. S. dos Santos e Ana M. D. Breda. A projeção estereográfica no GeoGebra. 1ª. Conferência Latino Americana de GeoGebra. ISSN 2237- 9657, pp.AA-BB, 2011.