 Na imagem visualizamos o logotipo do projeto 'MatematiZou', escrito com letras de forma na cor verde-azulada. A letra “Z” está na cor branca dentro de um hexágono com pontas arredondadas preenchido na mesma tonalidade de cor do restante das letras.  Na imagem temos um mini caminhão branco de madeira, cuja caçamba é azul escura e está escrito em letras brancas “UFABC”. As rodas do caminhão são vermelhas e quadradas. Cada par de rodas do caminhão está em cima de uma pista com ondulações.  Na imagem, há várias pessoas participando do evento “UFABC para todos” no Ginásio da UFABC campus Santo André. Algumas pessoas estão ao redor de uma mesa com jogos que incluem copos, mapas, tabuleiro de xadrez, entre outros, e outras, estão vendo as exposições espalhadas por todo o ambiente.](https://matematizou.gradmat.ufabc.edu.br/files/LogoMatematizouTeal.png)
Que história é essa?
Você já tentou colorir o mapa dos estados de um país usando somente 4 cores distintas de modo que estados vizinhos não fossem pintados com a mesma cor? Entende-se por estados vizinhos aqueles cujas representações no mapa tenham parte de sua fronteira em comum. Em 1852, Francis Guthrie realizou tal tarefa com o mapa dos distritos da Inglaterra. Ele então conjecturou que qualquer mapa poderia ser colorido utilizando apenas quatro cores. Ainda em 1852, muito animado ao saber dessa conjectura, De Morgan escreveu uma carta para Hamilton, o qual não achou o problema tão interessante.
Muitos matemáticos se aventuraram em estudar essa conjectura de Guthrie, mas uma prova de sua validade foi dada somente em 1976 por Appel e Haken, tendo sido necessárias mais de mil horas de cálculos por computadores. Em 1994, no Congresso Internacional de Matemática, em Zurique, Seymour, Robertson, Sanders e Thomas apresentaram uma nova demonstração ainda com auxílio de computadores, porém com cálculos mais simplificados. Até o presente momento não se conhece uma demonstração do teorema das quatro cores sem auxílio de computadores. No entanto, muitas aplicações, variações e generalizações do problema surgiram nas últimas décadas.
Descrição da atividade
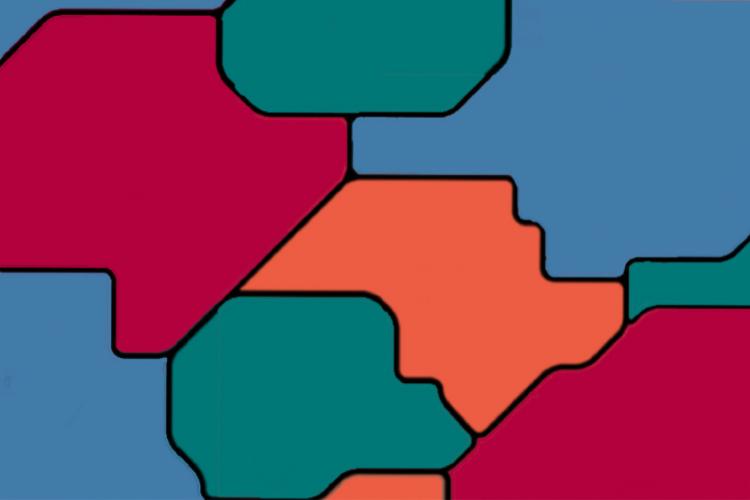
Você deve colorir todas as regiões abaixo usando apenas 4 cores, de modo que nenhuma região tenha a mesma cor de outra região com intersecção de fronteira.
Saiba mais
- Gerhard Ringel. Map Color Theorem, New York–Berlin: Springer-Verlag, 1974.
- Kenneth Appel, Wolfgang Haken. The Solution of the Four-Color-Map Problem, Scientific American, Vol. 237, No. 4 (October 1977), pp. 108-121.
- John Mitchem. On the History and Solution of the Four-Color Map Problem, The Two-Year College Mathematics Journal, Vol. 12, No. 2 (Mar., 1981), pp. 108-116.
Como fazer em casa / na escola
Variação 1:
Esta atividade deve ser aplicada a dois jogadores. Cada um deles recebe um mapa e 4 lápis nas cores vermelha, amarela, azul e verde. O objetivo é colorir o mapa usando todas as quatro cores e de modo que estados vizinhos, que compartilhem parte de sua fronteira, possuam cores distintas. Vence quem realizar tal tarefa corretamente.
Variação 2:
Uma alternativa para o jogo é tomar as seguintes peças construídas em madeira, cartolina ou EVA:
- seis peças retangulares com lados medindo 5 cm e 15 cm, sendo duas amarelas, duas azuis e duas verdes;
- seis peças retangulares de lados 5 cm e 10 cm, sendo duas azuis, duas vermelhas e duas verdes;
- seis peças quadradas com lados medindo 5cm, sendo três azuis, duas vermelhas e uma amarela.
O objetivo é construir um quadrado utilizando todas as peças e de modo que peças de mesma cor não tenham nenhum ponto de contato. Vence quem realizar tal tarefa corretamente.
