Flavius Josephus (Solução)

Recapitulando, os rebeldes judeus planejavam se organizar em um círculo, onde cada um teria a tarefa de matar o companheiro que estivesse à sua esquerda no sentido horário. Inicialmente, o judeu que estivesse na posição 1 deveria matar o que estivesse na posição 2 e, de igual forma, o sobrevivente que estivesse depois do primeiro a morrer, mataria o que estivesse vivo a sua esquerda no sentido horário. Esse processo continuaria até que apenas um judeu restasse, e esse último deveria cumprir o pacto com os demais, tirando a própria vida. No entanto, Josephus tinha outros planos e começou a pensar em qual posição ele deveria ocupar para garantir que seria o último sobrevivente, evitando assim que alguém o matasse. Ele não pretendia se suicidar.

Este é um problema matemático bastante interessante. A pergunta central é: “Qual seria a posição P do sobrevivente em um círculo com n pessoas se o processo se inicia na posição 1?”.

Esse problema não possui uma solução óbvia. Quando nos deparamos com um problema para o qual não temos uma ideia clara de como resolvê-lo, é promissor testar casos particulares e buscar padrões nas respostas. Para simplificar o problema, podemos analisá-lo para valores pequenos de n e observar os resultados. Vamos simular os primeiros valores:

– Para n = 1: não ocorre nada, pois apenas um rebelde está presente e ele sobrevive.
– Para n = 2: o rebelde na posição 1 mata o rebelde na posição 2. Portanto, o primeiro é o sobrevivente.

Vamos analisar mais alguns casos e começar a anotar essas simulações em uma tabela. (Sugerimos que use o simulador, mude os valores e observe o que acontece).

– Para n = 3: o primeiro mata o segundo, o próximo judeu é o terceiro, que mata o primeiro. Sobrevive o terceiro.

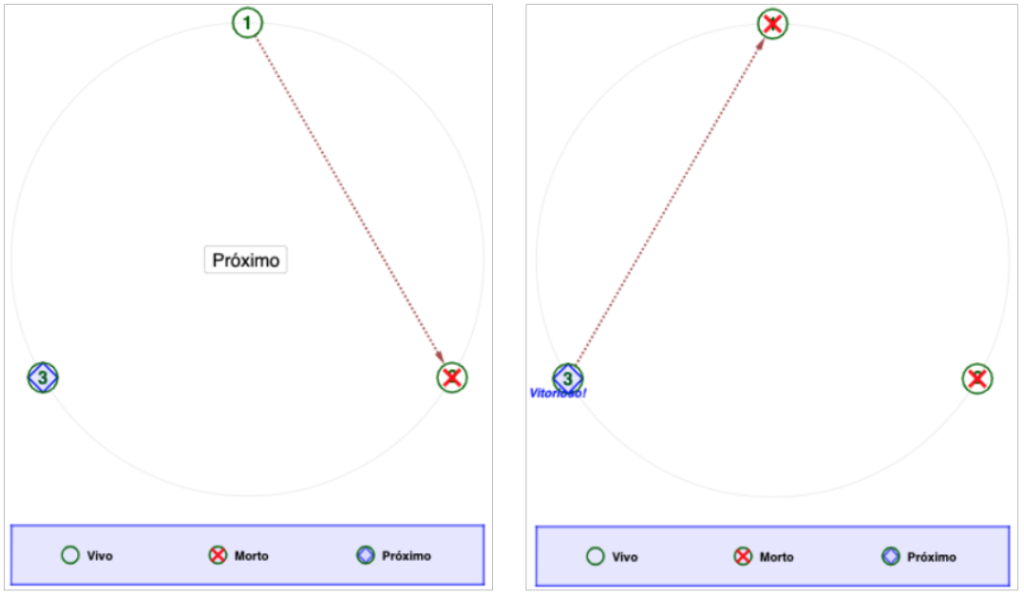
– Para n = 4: O primeiro mata o segundo, o terceiro mata o quarto; por fim, o primeiro mata o terceiro e sobrevive o primeiro.

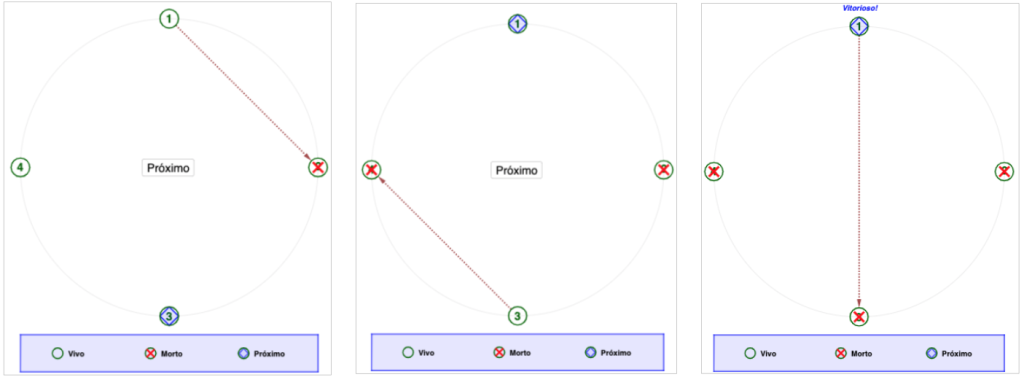
Até aqui isso ainda não é muito revelador, fazemos então mais alguns casos e preenchemos a planilha (confira os valores usando nosso simulador):

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	…
P_n	1	1	3	1	3	5	7	1	3	5	7	9	11	13	15	1	…

Agora, gaste um tempo analisando a tabela em busca de encontrar padrões…

• As posições dos sobreviventes são sempre ímpares, isso ocorre porque começamos com uma posição ímpar (1) e o processo de eliminação ocorre sempre em pares (um judeu mata o outro), de modo que na primeira rodada, todos os pares são eliminados;
• À medida que aumentamos o valor de n, a posição do sobrevivente parece seguir um padrão em forma de espiral: 1, 1, 3, 1, 3, 5, 7, 1, 3, 5, 7, 9, 11, 13, 15, 1. Eles crescem, volta a ser a posição 1, voltando a crescer de novo e a voltar para a posição 1;
• Quando o número total de pessoas no círculo é uma potência de 2, o sobrevivente estará sempre na primeira posição (posição 1), ou seja, a posição 1 é a ideal para n=1,2,4,8 que correspondem a potências de 2, 1=2^0, 4=2^2, 8=2^3, 16=2^4.

Da terceira observação, podemos supor que toda vez que o número de rebeldes for uma potência de 2, o sobrevivente vai ser a pessoa posicionada na posição 1. Embora isso seja verdade para os primeiros números da tabela, precisamos provar que vale sempre. Felizmente, para esse caso, podemos observar que se n for potência de 2, n=2^q e, na primeira rodada, todos os lugares pares são eliminados (o rebelde da posição 1 mata o da posição 2, o da posição 3 mata o da posição 4, o da posição 5 mata o da posição 6, assim por diante). 

Veja que na primeira rodada temos 2^q, na segunda rodada  n/2=2^q/2=2^{q-1}, pois morrem a metade… até que chegamos em 2^0=1, para algum número k de rodadas. Observe que em todos esses casos, cada rodada sempre inicia com o primeiro rebelde (nesse caso, o rebelde da posição 1). 

Exemplo: n=64 =2^6
1ª rodada: morrem 32 (o rebelde da posição 1 mata o da posição 2… o rebelde da posição 63 mata o da posição 64, encerrando a primeira rodada);
2ª rodada: inicialmente há 32 rebeldes e novamente se inicia com o rebelde da posição 1 matando (nesta rodada, ele mata o rebelde da posição 3), morrem 16;
3ª rodada: morrem 8;
4ª rodada: morrem 4;
5ª rodada: morrem 2;
4ª rodada: morre 1, restando o sobrevivente da posição 1.

Sabemos que a primeira posição é do sobrevivente sempre que n é uma potência de 2, mas o que acontece quando n não é potência de 2?

Podemos escrever um número qualquer n como a soma de uma potência de dois com outro número que é menor do que essa potência de dois, isto é, n = 2^k+r, com r < 2 ^ k. Parece complicado, mas vamos dar um exemplo. Tome n=19 e tome a maior potência de 2 que é menor do que 19.  Veja que estamos falando de 16=2^4, nosso r será 3, a diferença entre 19 e 16, e podemos então reescrever 19=16+3. Agora, o que ocorre depois que morrerem 3 pessoas dessas 19? Nesse caso restarão 16 pessoas, e sabemos que o primeiro que inicia a matança quando tem 16 pessoas (por ser potência de 2) é o sobrevivente. Para morrerem 3, é preciso que 3 os tenham matado, conforme Figura 3, nesse caso, restam 16 sendo que o primeiro a começar a matança é o da 7ª posição. Veja que r=3 e que o sobrevivente será o 2r+1 (o próximo a começar a matar quando restam 16 rebeldes).

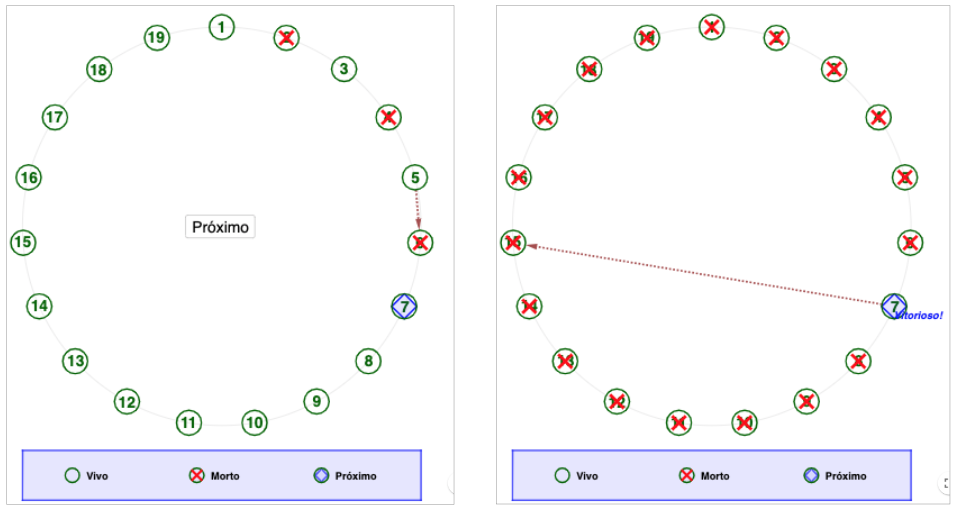
Vamos repetir o raciocínio para n=21. Nesse caso podemos reescrever n = 16+5 (ou n=2^4+5) e para morrer 5, teremos no último passo, o 9º matando o 10º, restando 16 rebeldes com o 11º sendo o próximo a matar, ou seja, o rebelde da 11ª é o primeiro a iniciar a matança entre os 16 e, como sabemos, será o sobrevivente. Veja a simulação da Figura 4.

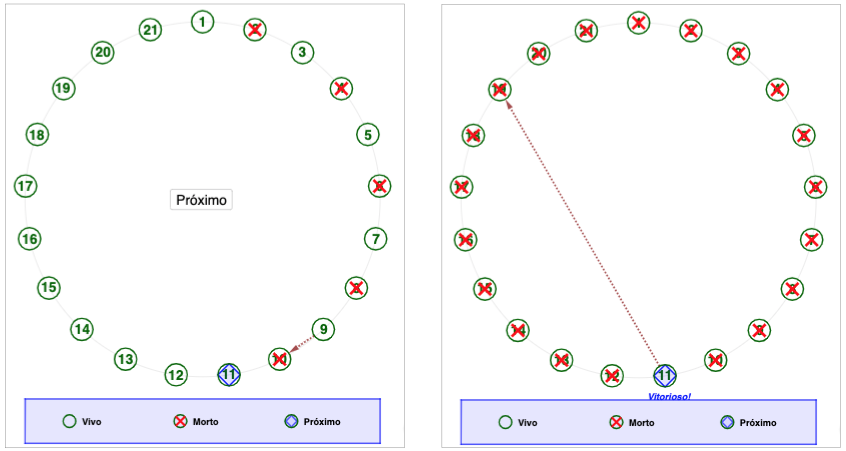
De um modo geral, sendo n o número de pessoas, escrevemos n=2^q + r, em que 2^q é a maior potência tal que 2^q \leq n. Nesse caso, o sobrevivente estará na posição 2r+1.