Para simplificar a resolução do desafio, é comum na matemática transformar um problema em outro equivalente, porém com um cenário mais simples. Inicialmente iremos numerar as casas do tabuleiro como na figura abaixo:

Observe agora que a casa 5 não pode ser alcançada pelo cavalo porque não há nenhum movimento que possibilite chegar nela a partir das posições em que os cavalos iniciam; veja que o cavalo sempre se movimenta em L e se algum cavalo se movimentasse de alguma casa para a casa 5, ele poderia retornar a essa casa. Mas, da casa 5 você não consegue ir a lugar nenhum fazendo o movimento em L.
Observe ainda que ao sair de uma casa ímpar você chega em uma par e ao sair de uma par você sempre chega em uma casa ímpar. Vamos escrever os movimentos possíveis dos cavalos que inicialmente estão nas casas 1,3,7 e 9:
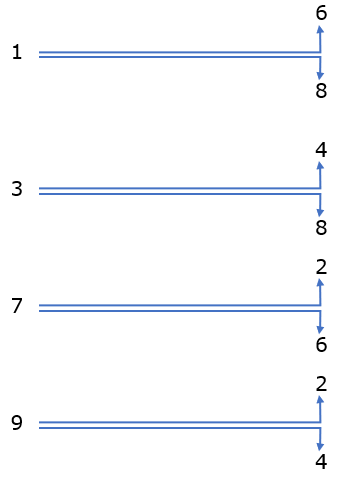
Após numerar as casas do tabuleiro e, em seguida, identificar as possíveis movimentações de cada cavalo a partir de uma casa numerada, podemos transformar o problema em um grafo, uma estrutura composta por pontos (vértices) e linhas (arestas), na qual cada movimento no tabuleiro corresponde a um movimento no grafo e vice-versa. Dessa forma, cada quadrado será representado por um vértice. Abaixo, temos o grafo da posição inicial das peças:
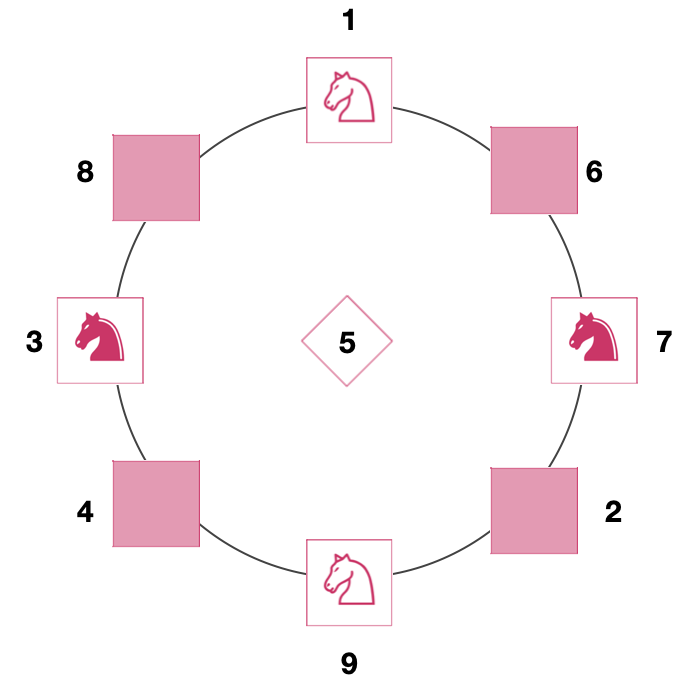
Também podemos considerar o grafo das possíveis posições finais dadas pelo desafio:
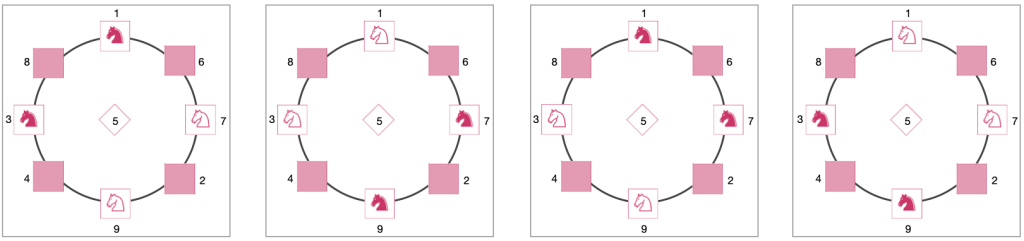
Agora a simplicidade do problema consiste em perceber que cada movimento do cavalo no tabuleiro corresponde a um movimento no grafo.
Se você tentou resolver o problema a partir de movimentos no tabuleiro, percebeu que é muito difícil decidir se o problema tem ou não solução, no entanto, ao olhar para as figuras dos grafos, note que a ordem em que os cavalos aparecem no círculo não pode ser mudada, já que um cavalo de uma cor não pode pular o cavalo da outra cor no círculo, com isso, o desafio proposto não tem solução.
 Na imagem visualizamos o logotipo do projeto 'MatematiZou', escrito com letras de forma na cor verde-azulada. A letra “Z” está na cor branca dentro de um hexágono com pontas arredondadas preenchido na mesma tonalidade de cor do restante das letras.  Na imagem temos um mini caminhão branco de madeira, cuja caçamba é azul escura e está escrito em letras brancas “UFABC”. As rodas do caminhão são vermelhas e quadradas. Cada par de rodas do caminhão está em cima de uma pista com ondulações.  Na imagem, há várias pessoas participando do evento “UFABC para todos” no Ginásio da UFABC campus Santo André. Algumas pessoas estão ao redor de uma mesa com jogos que incluem copos, mapas, tabuleiro de xadrez, entre outros, e outras, estão vendo as exposições espalhadas por todo o ambiente.](https://matematizou.gradmat.ufabc.edu.br/files/LogoMatematizouTeal.png)

