Quando coelhos e raposas se juntam à festa

Uma pergunta que surge sempre que resolvemos um problema como esse é: será que essa ideia pode ser replicada para outras versões do mesmo problema?

Considere, por exemplo, que o barqueiro precisa atravessar um coelho, uma cabra, um lobo, uma raposa e um cesto de repolho. As restrições são as seguintes:

• O lobo e a raposa comem o coelho;
• O lobo e a raposa também comem a cabra;
• A cabra e o coelho comem o cesto de repolhos.

O problema acima pode ser representado pela seguinte estrutura.

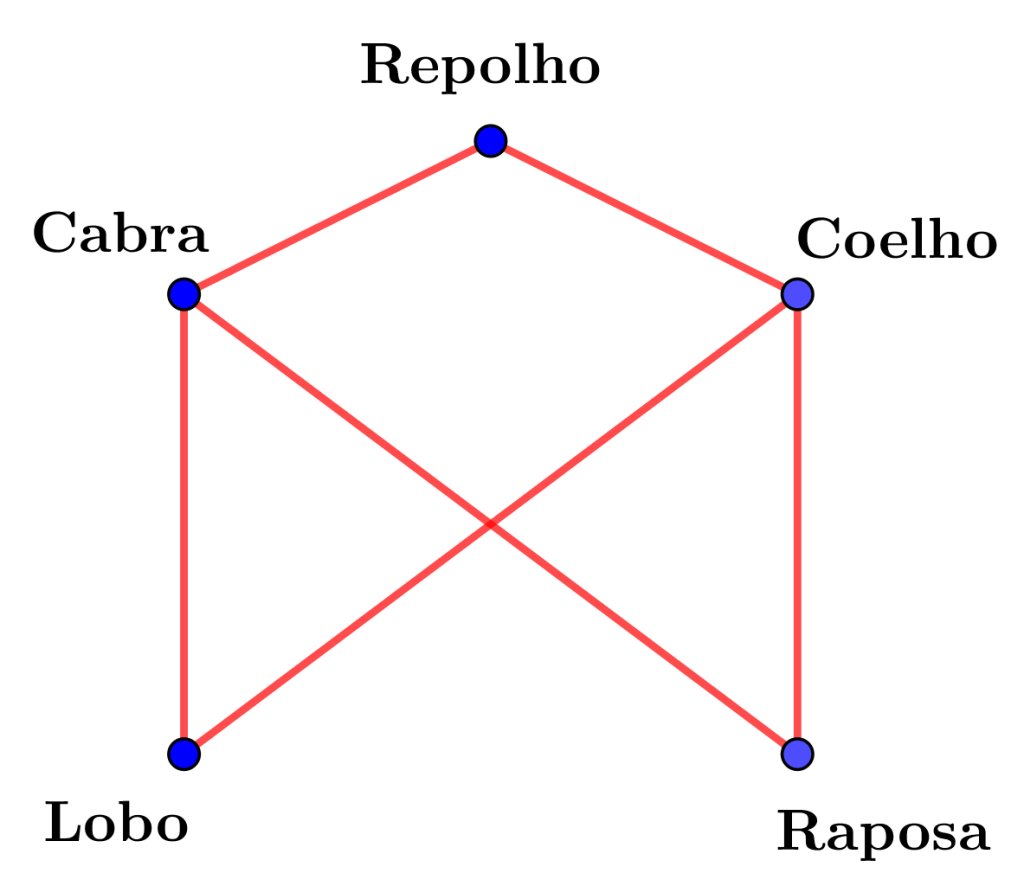
Olhando para a estrutura representada acima, responda: é possível atravessar todos em um barco com apenas um lugar?

Tome um tempo e pense sobre o problema, antes de prosseguir…

Para entender o que está acontecendo, tente aplicar a este problema o mesmo tipo de considerações que aplicamos ao anterior.

Conseguiu?? Se não, tente se fazer as seguintes perguntas:

• No problema original a cabra tinha um papel especial. Qual era esse papel?
• Algum passageiro nesta rede consegue representar o mesmo papel?
• Se não, o que isso significa?

Tome um tempo para pensar nestas perguntas antes de prosseguir…

A resposta resumida é que um barco de apenas um lugar é muito pequeno para o barqueiro transportar a todos com segurança!!

Para ver isso, basta voltarmos à rede acima e notar que retirar apenas um passageiro não é suficiente para resolver todos os conflitos! Sempre restarão personagens que não podem ficar juntos e sozinhos.

Mudemos então a pergunta!

Que tamanho de barco precisamos para resolver o problema? Será que com um barco de dois lugares o barqueiro consegue transportar a todos em segurança?

Use o aplicativo abaixo para tentar responder essa perguntas. Dica: encontre um par de personagens que quando afastados do grupo acabem com os conflitos.

Se conseguiu, parabéns!!

A resposta, de modo análogo ao problema original, passa por perceber que agora o par cabra/coelho quando afastado do grupo evita todos os conflitos.

Assim, qualquer solução deve manter este par afastado dos demais enquanto transportamos a todos, ou sob supervisão do barqueiro.

1. Abaixo colocamos uma solução possível! Volte ao aplicativo e tente replicar esta solução, observando como o par cabra/coelho está sempre afastado dos demais ou, caso estejam com outro personagem, estão sob a supervisão do barqueiro.
2. Coloque o par cabra/coelho no barco e os leve para o outro lado do rio;
3. Retorne com o barco vazio;
4. Coloque o lobo e a raposa no barco e leve-os para o outro lado do rio;
5. Deixe o lobo e a raposa na margem, e coloque cabra e coelho no barco;
6. Volte com o par cabra/coelho;
7. Deixe o par na margem e coloque o repolho no barco;
8. Leve o repolho para o outro lado;
9. Volte com o barco vazio para buscar o par cabra/coelho.

No próximo nível, inspirados pelo problema que acabamos de resolver, vamos mostrar algumas perguntas que matemáticos costumam fazer quando se deparam com este tipo de desafio.

Quando estiver pronto, basta clicar no botão abaixo!