Generalizando o Problema de Alcuin

Agora que resolvemos duas versões de um mesmo problema, é chegada a hora que matemáticos tanto esperam: a generalização!

Mas o que é isso?

O nosso primeiro instinto é de simplesmente ampliar o número de personagens, colocando relações de conflitos complicadas para, a seguir, tentar resolver o mesmo problema. Ou seja, dada um conjunto de personagens e conflitos e um barco, tentar transportar todos em segurança para o outro lado do rio.

Mas esse tipo de desafio, apesar de ser potencialmente divertido, vai ser tão complicado quanto as relações de conflitos que determinarmos, podendo ficar inviável quando tivermos muitos personagens e muitas relações.

As perguntas mais interessantes agora passam por entender o que é comum às diversas versões do mesmo problema. 

Coisas como, dado um conjunto de personagens e relações de conflitos o que podemos dizer sobre o tamanho do menor barco que consegue, em várias viagens, carregar a todos em segurança?

Note que responder essa pergunta não passa necessariamente por encontrar um modo de transportar as pessoas!

Podemos dizer, por exemplo, que o total de lugares livres no barco deve ser menor ou igual ao total de personagens. Isso por que um barco que caiba todos sempre consegue transportar o grupo em uma viagem.

A ideia agora é melhorar essa estimativa…

Esse é o tipo de pergunta que, em geral, os matemáticos gostam de responder.

Representando melhor o nosso problema

Antes de começar, vamos tentar deixar as coisas um pouco mais claras.

Nos problemas anteriores (problema original, segundo problema) fizemos uma representação dos conflitos entre personagens usando uma rede. Para isso substituimos os personagens por pontos e representamos a existência do conflito entre dois personagens por um segmento de reta ligando os pontos correspondentes.

As imagens abaixo mostram exemplos de algumas destas redes.

Na matemática este tipo de estrutura é conhecida como rede ou grafo. Os pontos são chamados de vértices, enquanto os segmentos são chamados de arestas.

Grafos são amplamente aplicados em diversas áreas da ciência e da própria matemática. Podem ser utilizados para representar circuitos elétricos, redes de computador, relações genealógicas, relações entre entradas de um banco de dados, modelagem de redes sociais, dentre milhares de outras aplicações.

Neste problema nossa intenção é representar os conflitos existentes entre personagens do problema de Alcuin, e por isso usaremos a expressão rede de conflitos ou grafo de conflitos.

Ótimo! Agora que temos o objeto que queremos estudar (a rede de conflitos) precisamos entender o que queremos saber.

Estamos interessados em saber qual o menor barco com o qual conseguimos resolver o problema de Alcuin. Ou seja, o menor barco com o qual conseguimos transportar todos em segurança.

Para simplificar, vamos desconsiderar o lugar do barqueiro. Ou seja, quando dissermos que um barco tem 3 lugares, estamos dizendo que o barco comporta o barqueiro e mais 3 personagens.

O problema original, por exemplo, era representado pela seguinte rede, que chamaremos de G:

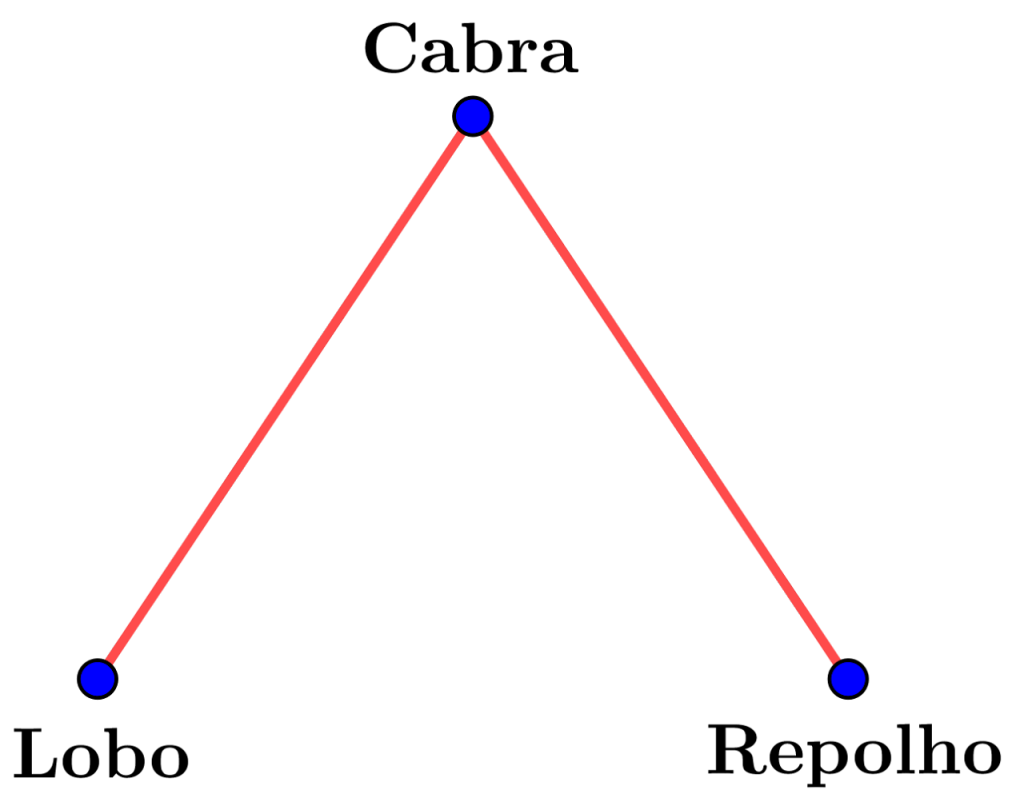
E o problema podia ser resolvido com um barco de apenas 1 lugar. 

Por essa razão dizemos que o número de Alcuin desta rede é 1, o que pode ser resumido na expressão al(G)=1.

Já o segundo problema era representado pela rede abaixo (que chamaremos de H).

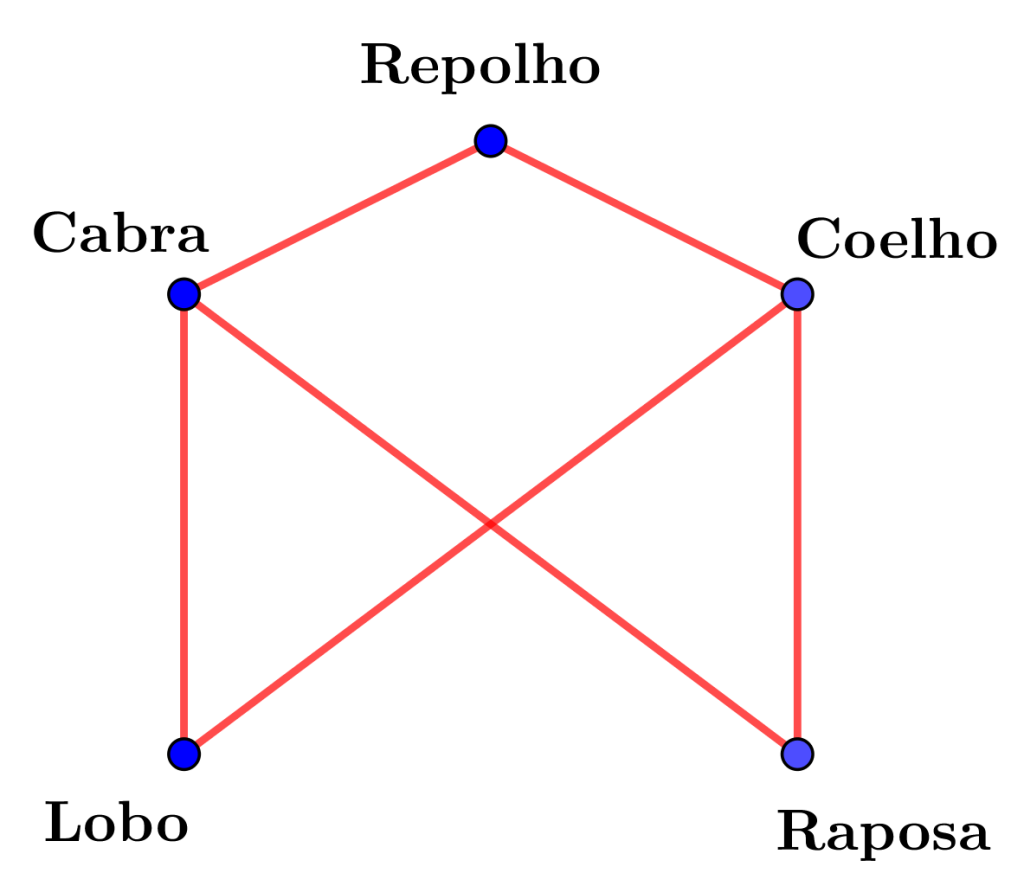
Para esta rede nós vimos que 1 lugar no barco não é suficiente, mas com 2 lugares o problema tinha solução.

E, portanto, o número de Alcuin desta rede é 2. Ou seja, al(H)=2.

Em outras palavras, dada uma rede de conflitos R chamaremos de número de Alcuin o menor número de lugares no barco para o qual o problema de Alcuin em R tenha solução, e denotaremos esse número por al(R).

Caminhando para a solução…

Até agora, representando os personagens e conflitos através de um grafo, resumimos nosso problema a encontrar o chamado número de Alcuin da rede. Ou seja, o total de lugares no menor barco com o qual conseguimos transportar todos em segurança para o outro lado do rio.

Comecemos com um comentário simples! É claro que se todos os conseguimos colocar todos os personagens no barco, então todos podem ser transportados em segurança!

Traduzindo a observação acima para uma rede de conflitos G temos a seguinte expressão:

al(G) ≤ número de vértices em G

Mas podemos fazer melhor do que isso!!

Para isso, voltemos ao último problema que analisamos. Nele trabalhamos com a rede da figura acima, e determinamos que al(G)=2.

Mas por que não conseguimos resolver o problema com um barco de apenas 1 lugar? Você lembra?

Se não lembra, pense um pouco mais sobre o problema antes de continuar! A resposta está logo na primeira travessia que fazemos com o barco. Pergunte-se: o que deve acontecer com a rede quando retiramos personagens do grupo e colocamos no barco? O que conseguimos fazer retirando 2 personagens que não conseguimos fazer com apenas 1?

Lembrou agora?

O que precisamos é que não existam conflitos entre os personagens que ficaram sozinhos na margem. Olhando para a rede G precisamos retirar dois vértices de modo que não exista aresta conectando os vértices restantes!

Veja abaixo o que acontece com a rede anterior quando retiramos a Cabra e o Coelho!

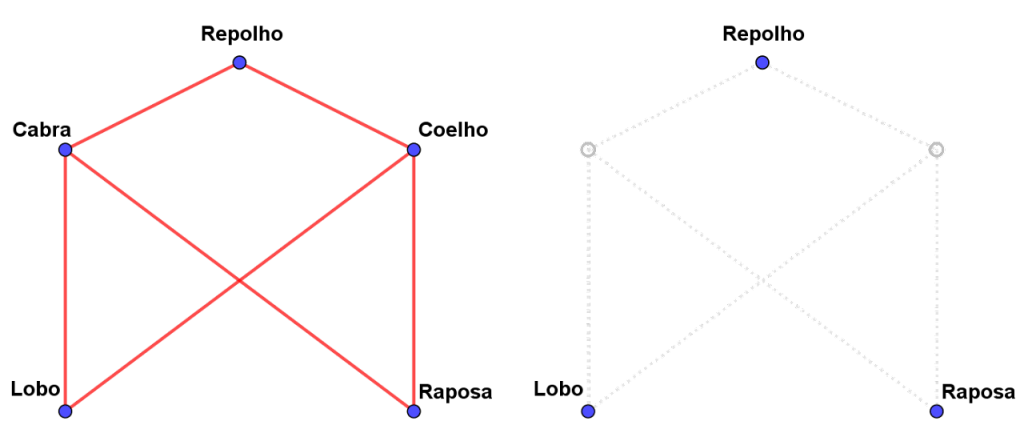
Um conjunto de vértices com essa propriedade é conhecido como cobertura da rede.

Assim, para determinar o tamanho do barco, precisamos encontrar uma cobertura da rede de conflitos. E se queremos o menor barco possível, precisamos saber o tamanho da menor cobertura possível da rede.

Na matemática temos um nome chique para a quantidade de vértices na menor cobertura de uma rede, que chamamos de número de cobertura minimal da rede.

Para que você entenda um pouco melhor este conceito, brinque um pouco com o aplicativo abaixo. Retire vértices da rede tentando encontrar a menor cobertura do grafo. Quando quiser, aperte o botão para mostrar uma cobertura mínima possível e descobrir o número de cobertura minimal da rede.

Ótimo!! Com isso vemos que o barco que resolve o problema deve ter espaço para comportar ao menos uma cobertura mínima da rede de conflitos. Ou seja,

al(G) ≥ número de cobertura minimal de G

Mas isso é sempre suficiente?? Sempre conseguimos transportar todos os passageiros com segurança usando um barco com tamanho exatamente igual ao da cobertura mínima?

Para entender este problema, considere a rede a seguir:

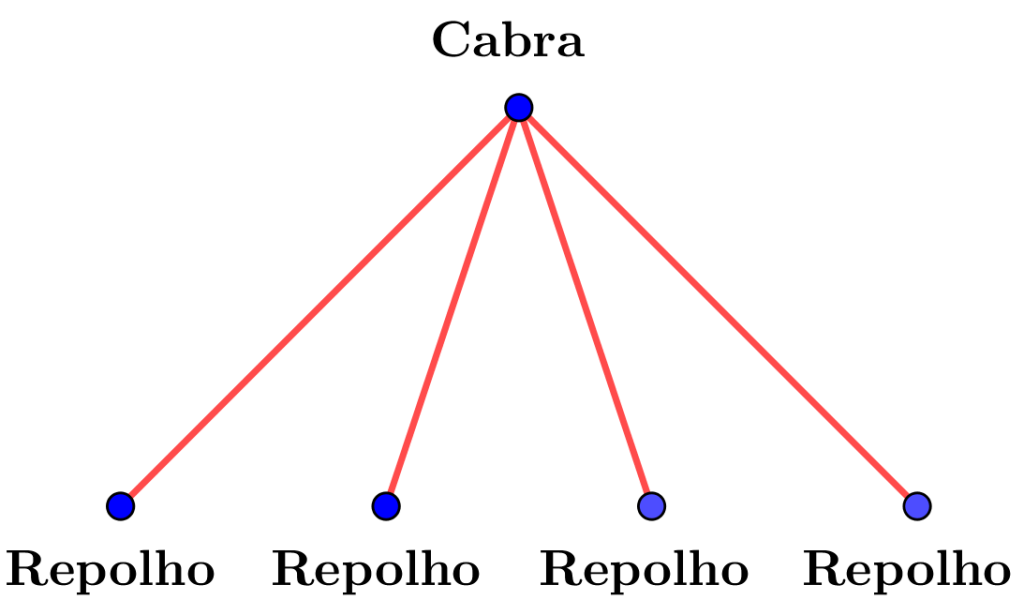
Antes prosseguir, pense um pouco sobre a rede acima…

Qual o número de cobertura minimal da rede?

Não deve ser difícil ver que retirando a Cabra, todos as arestas desaparecem! Com isso, o número de cobertura mininal desta rede é 1!

Mas conseguimos transportar todos os passageiros usando um barco com apenas um lugar??

Tente pensar um pouco sobre isso… Pegue um papel e uma caneta e desenhe o problema. Veja se consegue resolvê-lo.

Depois de algumas tentativas, você deve se convencer de que simplesmente não é possível resolver o problema representado pela rede acima com um barco de apenas 1 lugar!

Isso nos mostra que existem redes para as quais o número de Alcuin é estritamente maior que o número de cobertura minimal!

Mas o quão maior ele precisa ser??

Volte à rede da figura acima e tente responder esta pergunta. Você consegue resolver o problema do transporte com um barco de 2 lugares?