
Neste problema faremos uma viagem no tempo!
Começaremos no século VIII d.C., quando um acadêmico da corte de Carlos Magno, Alcuin de York, propõe um simples problema sobre o transporte de cabras, lobos e repolhos através de um rio.
Após uma breve pausa, onde aproveitaremos para mexer e complicar um pouco no
problema colocado por Alcuin, pousaremos no século 21! Mais precisamente no ano de 2008, quando um grupo de matemáticos modernos resolve complicar ainda mais o problema milenar, colocando uma pergunta aparentemente mais complicada, mas com uma resposta impressionantemente simples!
Vamos começar!
O problema original de Alcuin – ou a cabra, o lobo e os repolhos
O problema que descrevemos abaixo foi proposto um Alcuin de York, um monge e intelectual Anglo-Saxão do século VIII d.C..
Comecemos por um desafio…
Um barqueiro precisa levar para a outra margem de um rio uma cabra, um lobo e um cesto de repolhos.
Isso seria uma tarefa fácil, se seu barco não fosse tão pequeno. De fato, o barqueiro não consegue carregar mais que um destes passageiros de uma só vez.
Para piorar, seus passageiros não sabem se comportar sem supervisão. A cabra, se deixada sozinha com o cesto de repolhos, comerá todos. E isso se não for devorada antes pelo lobo, que também não consegue se controlar quando afastado do olhar atento do barqueiro.
Com isso, o desafio está posto: como levar todos de um lado ao outro do rio?
O barqueiro pode fazer diversas viagens, mas levando consigo apenas um passageiro por travessia. Em nenhum momento o lobo e a cabra podem ficar sozinhos. E o mesmo vale para a cabra e o cesto de repolhos.
A simples presença do barqueiro na mesma margem do rio é o suficiente para coibir os instintos naturais da cabra e do lobo.
Você consegue ajudar o barqueiro??
Você pode tentar fazer isso apenas com papel e caneta. Usar objetos diferentes para representar cada passageiro pode ser útil!
Para simplificar, fizemos um pequeno aplicativo onde você pode explorar este problema!
Instruções:
1. Clique em um passageiro para colocá-lo no barco;
2. Pressione o botão “Atravessar/Voltar” para levar o barco para o outro lado do rio;
3. Clique no passageiro dentro do barco que desembarcá-lo na margem correspondente.
Agora que você já explorou o problema, prossigamos!
Você conseguiu resolver o desafio? Se sim, parabéns!! Se não, não tem problema! Sigamos com a atividade, que as coisas ficarão mais claras.
Antes de mais nada tente responder as seguintes perguntas:
• Dentre os três passageiros, existe um deles que é a chave para a solução. Você sabe dizer que passageiro é esse?
• Por que o passageiro acima é tão importante?
Volte ao problema (pode usar o aplicativo!) e explore o problema tendo as perguntas acima na cabeça.
E agora? Conseguiu??
Quando achar que já pensou o suficiente sobre as questões acima, clique aqui para a resposta!
O personagem central no problema é a cabra! É o único dos passageiros que, ao ser afastada do grupo, resolve todos os conflitos.
A solução, portanto, tem que manter a cabra sempre acompanhada do barqueiro ou separada dos demais passageiros!!
Se ainda não resolveu, volte ao problema mais uma vez e tente..
Encontrando uma melhor representação
Se ainda não foi desta vez, vamos dar mais uma ajuda!!
Para melhor responder as perguntas acima, vamos encontrar uma representação mais adequada para o nosso problema.
Começaremos por representar cada um dos passageiros por um círculo (ou apenas um ponto). Vamos também ligar através de uma seta todo par de passageiros que não pode ficar sozinho.
Deste modo, colocaremos uma seta apontando do lobo para o coelho e outra do coelho para o repolho, como na imagem abaixo.
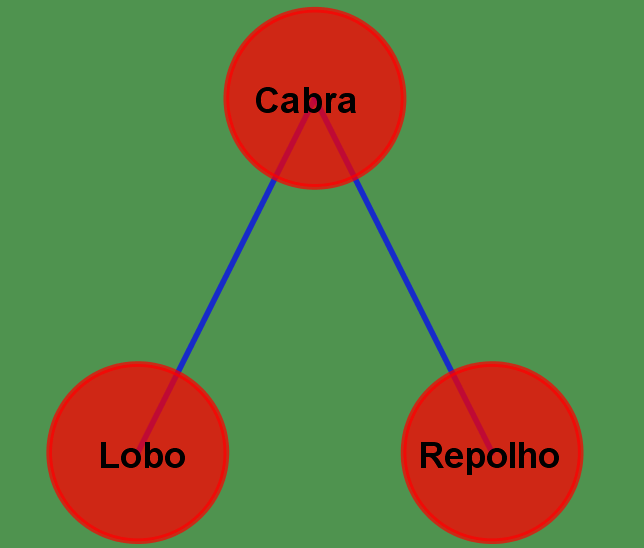
Usando agora o aplicativo abaixo, tente novamente resolver o problema, focando agora nas perguntas feitas acima.
Quando achar que já pensou o suficiente sobre as questões acima, clique aqui para mais dicas!
Ao tirarmos apenas o repolho ou o lobo, o par que resta na margem do rio ainda é problemático! A cabra é a única cuja retirada resolve todos os conflitos! Ela é, portanto, o foco de nossa dor de cabeça. No momento que o isolamos dos demais, podemos ficar despreocupados.
Se você ainda não resolveu o problema, ainda dá tempo! Volte ao aplicativo e tente resolver tendo em mente o papel da cabra.
Resolvendo o Problema
Agora que entendemos o papel central da cabra no problema, a solução fica mais acessível.
Já sabemos que qualquer solução precisa manter a cabra sempre afastada de seus companheiros, seja sozinha no barco ou em uma das margens do rio.
Abaixo propomos uma solução possível para o problema! Tente replicar a solução abaixo no aplicativo e veja como deixamos a cabra sempre afastada de todos.
Veja a Solução:
- Começamos levando o coelho para o outro lado.
- Em seguida, retornamos e levamos o lobo.
- Ao deixar o lobo, trazemos o coelho de volta.
- Deixamos o coelho sozinho, e levamos apenas o repolho..
- Para finalizar, voltamos para buscar o coelho solitário.
Pronto! O problema está resolvido!
Vamos agora deixar o problema um pouco mais complicado! Quando estiver pronto, siga para a próxima parte abaixo.
Saiba mais
O problema que acabamos de apresentar era apenas um entre 56 problemas de matemática recreativa do livro Propositiones ad Acuendos Juvenes(Problemas para aperfeiçoar a juventude), escrito pelo próprio Alcuin. Nele existem mais duas variantes do problema da travessia do lobo, da cabra e do repolho:
1)Problema dos maridos ciumentos.
Na margem de um rio se encontram três homens e suas respectivas esposas. Eles devem atravessar o rio por meio de um bote em que só cabem 2 pessoas. Essa travessia tem que ser feita de tal maneira que uma mulher, cujo marido não está presente, nunca seja deixada ao lado de outro homem. Como realizar essa travessia?
2)Problema da Família.
Na margem de um rio se encontram um homem, sua esposa e seus dois filhos. O homem e a mulher possuem pesos iguais. Cada uma das crianças pesa a metade de um adulto. A travessia deve ser feita em um bote que suporta apenas o peso de um adulto. Como atravessar a família para a outra margem?
Tentem resolver essas variantes. Para saber mais sobre outros problemas do livro vejam esse link : https://en.wikipedia.org/wiki/Propositiones_ad_Acuendos_Juvenes
Como fazer em casa / na escola
O problema da travessia do lobo, da cabra e do repolho e seus outros variantes não exigem a manipulação de materiais. O máximo que se precisa é de um lápis e papel para rascunhar as possíveis soluções. Baseado nisso, como proposta para atividades em casa basta reunir familiares e amigos e apresentar os problemas para que pensem neles. Quanto a atividades em escola sugere-se ao professor apresentar o problema em sala de aula e propor para que seus alunos tentem resolvê-los.
 Na imagem visualizamos o logotipo do projeto 'MatematiZou', escrito com letras de forma na cor verde-azulada. A letra “Z” está na cor branca dentro de um hexágono com pontas arredondadas preenchido na mesma tonalidade de cor do restante das letras.  Na imagem temos um mini caminhão branco de madeira, cuja caçamba é azul escura e está escrito em letras brancas “UFABC”. As rodas do caminhão são vermelhas e quadradas. Cada par de rodas do caminhão está em cima de uma pista com ondulações.  Na imagem, há várias pessoas participando do evento “UFABC para todos” no Ginásio da UFABC campus Santo André. Algumas pessoas estão ao redor de uma mesa com jogos que incluem copos, mapas, tabuleiro de xadrez, entre outros, e outras, estão vendo as exposições espalhadas por todo o ambiente.](https://matematizou.gradmat.ufabc.edu.br/files/LogoMatematizouTeal.png)

