Batimento

Oscilações harmônicas
Oscilações são processos caracterizados por alguma medida de repetição, como por exemplo, o balançar de um pêndulo. As oscilações mais simples que aparecem na natureza são as chamadas oscilações harmônicas. Estas são oscilações tais que a quantidade que está oscilando, como o ângulo de deflexão de um pêndulo, muda com o tempo de acordo com a função seno ou cosseno (no caso do pêndulo, quando a amplitude é pequena).

São importantes por dois motivos:

• As oscilações na natureza são frequentemente muito parecidas com oscilações harmônicas;
• Fenômenos oscilatórios mais complexos podem ser representados por superposição de muitos osciladores harmônicos.

Representação matemática:

Um oscilador harmônico pode ser representado pela função real

x (t) = A \cos (\omega t + \alpha),

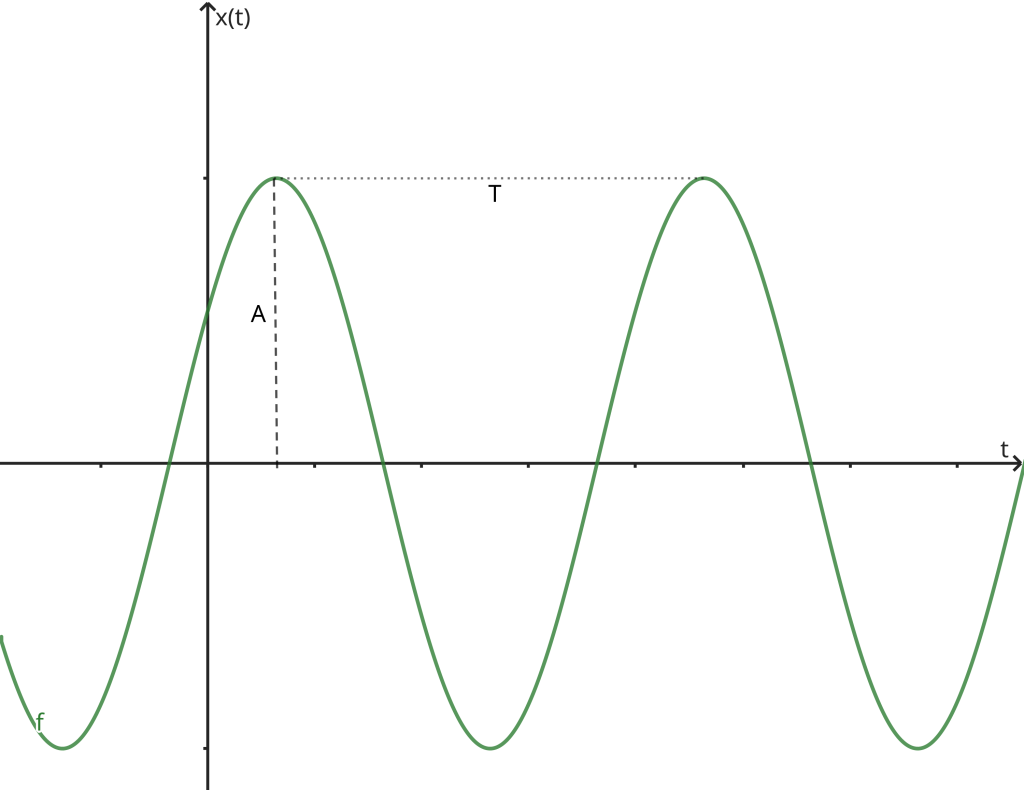
Como a função cosseno está limitada entre +1 e −1, os valores de x variam entre +A e −A. O número A é positivo, e corresponde à maior variação possível da oscilação em relação ao seu valor de equilíbrio, e é chamado de amplitude. O argumento do cosseno, \omega t +\alpha, é chamado de fase da oscilação.

Como a função cosseno é periódica de período 2\pi, diferentes posições x do oscilador irão se repetir no intervalo de tempo T em que a fase recebe um incremento de 2\pi. O intervalo T é chamado de período da oscilação que nos leva à condição.

x (t + T ) = x (t) \Leftrightarrow (t + T ) + \alpha =t+ \omega t + \alpha + 2\pi\Leftrightarrow T =\frac{2\pi}{\omega}

A frequência \nu de oscilação é definida como sendo o número de oscilações por unidade de tempo, i.e., \nu = \frac{1}{T}. Assim, \omega = \frac{2\pi}{T} é o número de oscilações em 2\pi unidades de tempo, também chamada de frequência angular.

Batimento

Um caso especial ocorre quando dois osciladores harmônicos x_1(t) e x_2(t) são somados com frequências próximas. O movimento resultante pode ser considerado como o de um único oscilador harmônico com amplitude pulsante. Essas oscilações são chamadas batimentos.

Seja \omega a frequência angular do oscilador x_1 e \omega + \delta\omega a frequência angular do oscilador x_2, então a soma deles é

x(t) = x_1(t) + x_2(t) = A \cos(\omega t) + A \cos((\omega + \delta\omega) t),

onde, por simplicidade, escolhemos a fase inicial como sendo nula nos dois osciladores. Usando a identidade trigonométrica

\cos(a) + \cos(b) = 2 \cos\left(\frac{a+b}{2}\right) \cos\left(\frac{a-b}{2}\right),

temos

x(t) = 2A \cos\left(\frac{\delta\omega}{2} t\right) \cos(\omega t + \phi),

onde \phi = \frac{\delta\omega}{2}t é a fase inicial do batimento. Assumindo que \omega é muito maior que \delta\omega, \omega \gg \delta\omega, temos

x(t) = 2A \cos\left(\frac{\delta\omega}{2}t\right) \cos(\omega t).

cujo gráfico pode ser representado por

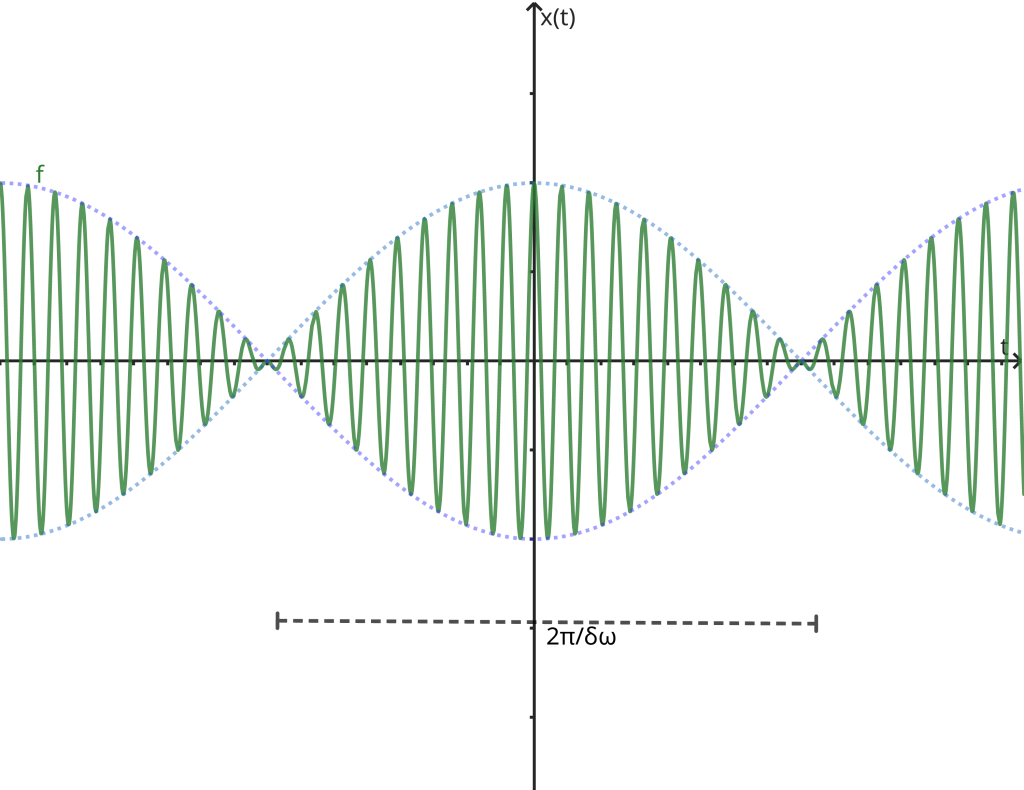
Na figura podemos observar que devido à condição \omega \gg \delta\omega, o termo \cos(\omega t) efetua várias oscilações completas ao passo que o fator 2A\cos(\frac{\delta\omega}{2}t) praticamente permanece inalterado. Então podemos interpretar x(t) como um oscilador harmônico de frequência \omega, cuja amplitude varia segundo uma lei periódica. A amplitude de oscilação deve ser positiva, portanto:

Amplitude = |2A \cos(\frac{\delta\omega}{2}t)|.

A frequência angular de oscilação da amplitude é o dobro da frequência de oscilação do fator 2A \cos(\frac{\delta\omega}{2}t). Isto é, a frequência angular da amplitude é \delta\omega, igual à diferença entre aquelas dos osciladores x_1 e x_2. O período dos batimentos será, portanto, T=\frac{2\pi}{\delta\omega}.

Aplicação

O fenômeno de batimento é comumente utilizado por músicos para afinar seus instrumentos por intermédio de um diapasão,

O diapasão está calibrado para oscilar a uma frequência especifíca (Lá 440Hz). Ao aproximá-lo de uma corda vibrante que vibra a uma frequência ligeiramente distinta do diapasão (a corda que sequer afinar), um batimento irá se pronunciar, como descrito acima. Ao ajustar tensão da corda para que sua frequência de vibração fique igual à frequência de oscilação do diapasão, a diferença entre
as frequências, \delta\omega, tende a zero, fazendo desaparecer o batimento. Nesse momento, considera-se afinada a corda.

Vamos testar?

Abaixo, podemos escolher a frequência das duas ondas geradas, ver o gráfico resultante (o número de oscilações no gráfico está reduzido para melhorar a visualozação) e até ouvir a onda sonora gerada, o batimento!

Como atividade, tente calcular o período a partir dos números que escolheu, no exemplo abaixo temos: T=|\frac{1}{\nu_1-\nu_2}|.