Pi(π) – o número

Pi (π ) é a constante matemática mais reconhecida no mundo. Muitos cientistas consideram Pi o número mais importante e intrigante em toda a matemática. O que é número pi? Ele é um número irracional cujo valor é 3,14159265358979323846. . . (e, por aí vai, ela nunca chega ao fim).

A indiana Sharma Suresh Kumar mantém o atual recorde do Guinness World Records por recitar a maior sequência dos dígitos de Pi. Ela recitou, com sucesso, 70.030 números em 17 horas e 14 minutos. O recorde de algarismos obtidos computacionalmente foi obtido pela equipe liderada pelo suíço Thomas Keller com exatos 62.831.853.071.796 dígitos em 2021.

Como calcular?

O valor de pi é obtido ao dividir o comprimento de uma circunferência pelo diâmetro.

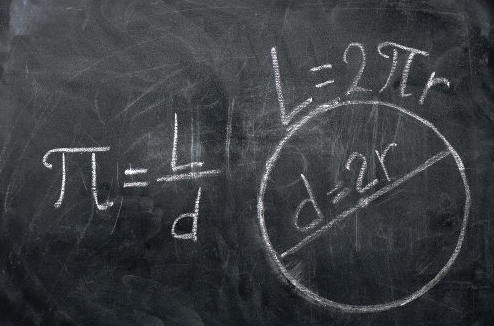
Algumas curiosidades…

• O Pi foi estudado pela raça humana por quase 4.000 anos. Por volta de 2000 a.C., os babilônios estabeleceram a razão constante de um círculo como 3-1/8 ou 3,125. Os egípcios antigos chegaram a um valor ligeiramente diferente, de 3-1/7 ou 3,143.

• O símbolo para o Pi (π) tem sido usado regularmente em seu sentido matemático apenas nos últimos 250 anos.

• No episódio de Star Trek “Wolf in the Fold”, Spock elimina o maligno computador ordenando que ele compute qual é o último dígito do valor de Pi.

• Os primeiros 144 dígitos de Pi somam 666 (o que muitos estudiosos dizem ser “a marca da Besta”). E 144 = (6+6) x (6+6).

• Em 1888 um médico de Indiana – EUA, Edward Johnson Goodwin, afirmou ter conseguido “enquadrar” o círculo. Em seu modelo, obteve \pi=3,2. Dez anos depois, por meio do representante Taylor Record, apresentou à Assembleia Geral de Indiana o projeto de lei em que proclamavam como verdade definitiva o valor 16/5 para a constante. O projeto foi aprovado por unanimidade na câmara de representantes na Assembleia…

Atividade – “Pesando π”

Vamos a aproximar π pesando um círculo e um quadrado!! Mas como? Vamos comparar um círculo de raio r e um quadrado de lado 2r. Observemos a figura abaixo:

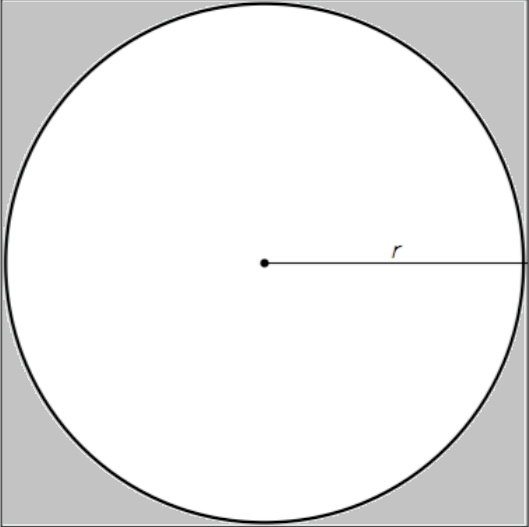
Agora obtenha, de alguma maneira, um círculo e um quadrado com as proporções acima. Uma ideia simples seria cortar círculos inscritos a partir de folhas quadradas, idealmente várias unidades. Outra possibilidade seria a impressão em uma impressora 3d de círculos e quadrados (no caso, claro, seriam peças com a mesma espessura e programadas para que o diâmetro do círculo seja igual ao lado do quadrado). Diversas ideias podem ser pensadas, formas de gelo, caixinhas cheias de areia, etc. Mas… como funciona?

Vamos calcular a massa das peças:

M_\bigcirc=\sigma A_\bigcirc,\;\; M_\Box=\sigma A_\Box

Nesse caso, consideramos \sigma uma constante que pode ser pensada como a densidade superficial do objeto que deve ser a mesma para os dois (o significado físico dessa constante depende da forma como será realizado o experimento mas, essencialmente, está associado ao material e à espessura da peça). As áreas respectivamente do círculo e do quadrado serão:

A_\bigcirc=\pi r^2,\;\; A_\Box=(2 r)^2.

A razão das massas, portanto, será:

\dfrac{M_\bigcirc}{M_\Box}=\dfrac{\sigma A_\bigcirc}{\sigma A_\Box}=\dfrac{\cancel{\sigma}\pi \cancel{r^2}}{\cancel{\sigma} 4 \cancel{r^2}}=\dfrac{\pi}{4}.

Agora, é usar a criatividade, pesar as massas, dividir e multiplicar por 4 e, voilà, teremos uma aproximação para \pi.

Como dica para atividade em sala de aula, seria interessante aproveitar o experimento para se falar de estatística, erros experimentais, etc. Ao se usar folhas, por exemplo, mostrar à turma como a aproximação funciona melhor quanto maior o número de folhas pesadas. Como evitar a influência de cortes descuidados na hora de se obter a média, será mediana a melhor saída? Vale a pena pesar várias unidades de uma única vez?

Abaixo, um vídeo com experimento realizado com peças impressas.

Saiba mais:

Apresentando o número pi – Portal da Matemática OBMEP:
https://www.youtube.com/watch?v=S9KBT3xB5b0

Demonstração da área do círculo – Matemática Criativa:
https://www.youtube.com/watch?v=q-S7m7yGB6Y

COMO CALCULAR o PI arremessando FÓSFOROS? (Agulha de Buffon) – Tem Ciência:
https://www.youtube.com/watch?v=vPre iDeNc

Saiba onde sua data de nascimento aparece nas casas decimais de pi utilizando o site Atractor:
https://www.atractor.pt/mat/fromPI/PIsearch.html

Como fazer em casa / na escola:

Aqui está uma sugestão de como replicar o experimento na sua casa:

Equipamentos: 

• balança digital;
• calculadora;

Materiais: 

• Dois potes, um em formato cúbico e outro cilíndrico (é importante que o pote de base quadrada  “circunscreva” o pote de base circular, como na figura apresentada no vídeo);
• Feijões (podem ser substituídos por arroz, areia, etc). A quantidade necessária dependerá da precisão da balança utilizada;

Passo a passo:

Preencha o pote cilíndrico com feijões, tendo cuidado para preenchê-lo até a borda. Em seguida, utilize uma balança para pesá-lo (se a sua balança for corporal, suba com o pote na balança e depois desconte o seu peso). Anote os valores e repita o procedimento com pote cúbico (preenchendo-o com a mesma altura do pote cilíndrico). Por último, realize os cálculos propostos para encontrar o valor aproximado de pi.