 Na imagem visualizamos o logotipo do projeto 'MatematiZou', escrito com letras de forma na cor verde-azulada. A letra “Z” está na cor branca dentro de um hexágono com pontas arredondadas preenchido na mesma tonalidade de cor do restante das letras.  Na imagem temos um mini caminhão branco de madeira, cuja caçamba é azul escura e está escrito em letras brancas “UFABC”. As rodas do caminhão são vermelhas e quadradas. Cada par de rodas do caminhão está em cima de uma pista com ondulações.  Na imagem, há várias pessoas participando do evento “UFABC para todos” no Ginásio da UFABC campus Santo André. Algumas pessoas estão ao redor de uma mesa com jogos que incluem copos, mapas, tabuleiro de xadrez, entre outros, e outras, estão vendo as exposições espalhadas por todo o ambiente.](https://matematizou.gradmat.ufabc.edu.br/files/LogoMatematizouTeal.png)
Uma prancha desliza sobre rodas, sempre paralela e à mesma distância da base. Entretanto, as rodas não são redondas! O que está acontecendo?
O engenheiro Franz Reuleaux (séc. XIX, alemão, mas pronuncia-se “rolô” com “r” enrolado e primeiro “o” puxado para “â”) desenvolvou vários mecanismos de transformação de movimento.
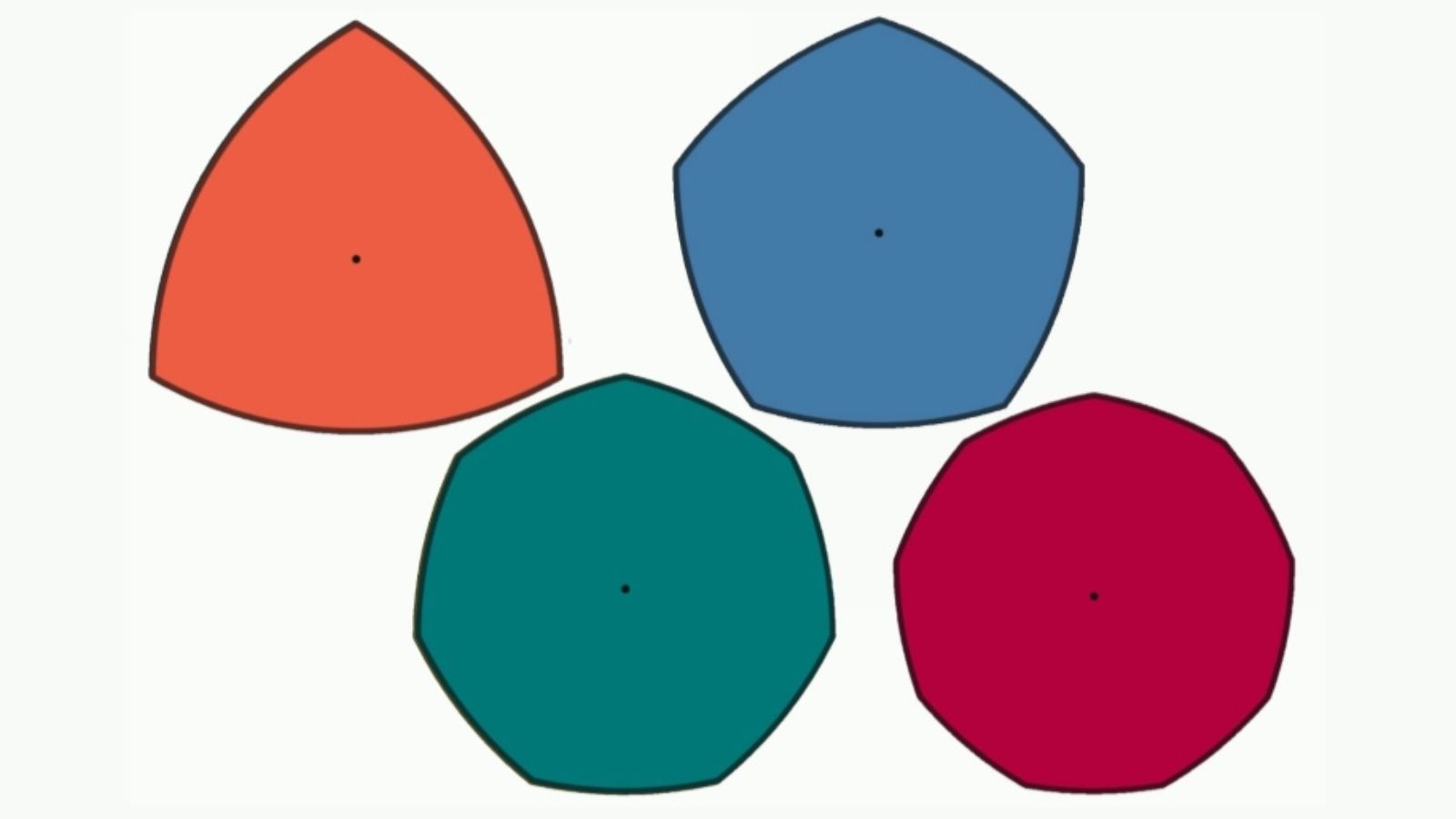
Para construir um triângulo de Reuleaux, comece com um triângulo equilátero de lado L. Com centro em cada vértice, abra o compasso e descreva o (menor) arco de círculo que passa pelos dois outros vértices. A curva fechada resultante tem “largura constante” L, que é a distância entre as duas tangentes paralelas. A construção pode ser generalizada a outros polígonos e (após algumas intervenções) também a poliedros.
Note que, conforme rola, o eixo da “roda” de Reuleaux sobe e desce, de modo que um carro com tais rodas trepidará em uma rua plana. Por outro lado, no caso da prancha apoiada sobre cilindros com tal secção, o
rolamento tem dois pontos de equilíbrio estático, um estável (com o eixo mais baixo e de interesse prático) e outro instável (com o eixo mais alto).
Toda curva de largura constante pode ser inscrita em um quadrado e girar dentro dele (com deslizamento), embora, novamente, seu centro não se mantenha fixo. Algumas brocas para abrir furos poligonais são fabricadas segundo esse princípio.
Construção do Polígono
Polígono girando
Para saber mais
A ideia dos polígonos de Reuleaux e das figuras de diâmetro constante é bastante interessante e traz muitas aplicações para ensino médio.
Temos vários exemplos de objetos cotidianos onde esse tipo de figura é encontrada e alguns exercícios com curvas de diâmetro constante no artigo Polígonos de Reuleaux e a generalização de Pi, escrito por José Luiz Pastore Mello e publicado na RPM 81. Esse artigo traz ainda uma generalização do pi para outras figuras diferentes do círculo.Respondendo a um dos problemas propostos no artigo da RPM, temos o artigo Triângulos de Reuleaux escrito por Sérgio Dantas, que apresenta uma proposta de construção dos polígonos de Reuleaux utilizando o Geogebra.
Como fazer em casa / na escola
Desenhar polígonos de Releaux com régua e compasso é relativamente simples, como podemos ver no applet “construção do polígono” acima. Aqui o mais interessante é a verificação de como o polígono construído dessa forma pode girar entre planos paralelos.
Existem diversas construções possíveis dependendo dos materiais e ferramentas disponíveis. O ideal é que os polígonos possam ser construídos em um material que não se deforme, porém na impossibilidade de trabalhar com tais materiais sugerimos uma construção “planificada” que pode ser feita até em EVA.
Você pode montar as molduras em EVA ou papel cartão (fica melhor se for papelão de caixa, tipo de supermercado), fixá-las em uma base de papel ou cartolina de forma em que fiquem paralelas e com distância igual ao diâmetro dos polígonos construídos.
Os polígonos devem recortados no mesmo material, e podem ser fixados pequenos pinos (no próprio material utilizado) que permitem o giro manual dos polígonos dentro das molduras.
No caso dessa construção simplificada os polígonos somente podem deslizar apoiados.
Além dessa possibilidade, podemos utilizar ferramentas computacionais como o geogebra, como pode ser visto nesse artigo. Ou ainda, caso sua escola disponha de uma impressora 3D os materiais apresentados a seguir podem ser impressos.
Caso disponha de materiais e ferramentas mais sofisticados temos algumas sugestões de construções interessantes que podem ser feitas com os polígonos de Releaux:
