Flavius Josephus

Contexto Histórico

Também conhecido pelo nome hebraico de Yosef Ben Mattityahu (José, filho de Matheus), Flavius Josephus foi um historiador judaico-romano que viveu no primeiro século da era cristã.

Por volta do ano 66 eclode a revolta de judeus contra Roma. Um dos episódios marcantes desta guerra é a disputa por Massada, fortaleza construída cerca de um século antes por Herodes, o Grande, no alto de uma montanha, em pleno deserto.

Um grupo de rebeldes conseguiu fugir com suas famílias do cerco de Jerusalém e refugiou-se em Massada. As legiões romanas sitiaram a fortaleza. Improvisando uma rampa em uma parte mais erodida da montanha, subiram com torres de assalto.

Cientes da derrota iminente, Jair, o líder dos rebeldes, discursou: “Nascemos livres e morreremos livres”. No judaísmo, o suicídio é algo inadmissível. Então cada rebelde foi até sua família e a matou. Então um homem foi matando outro até restar um, que se suicidou.

Com a deflagração da revolta, as circunstancias levam Yosef Ben a tomar parte no conflito. Em Jotapata, na Galiéia, Yosef Ben encontrava-se sitiado pelas tropas de Vespasiano com quarenta homens em uma cisterna. Então bradou: “Faremos como em Massada”. Porém ao restar apenas ele e outro soldado, Yosef convenceu-o a render-se. Este fato, aliado ao de agir com negociador com a resistência em Jerusalém e tornando-se, após isto, cidadão romano, com o nome latino de Flavius Josephus, e protegido dos imperadores Vespasiano, Tito e Domiciano, fez com que fosse visto como um pária por muitos judeus. Ironicamente, a história de Massada só chegou até nós por um de seus textos: A Guerra dos Judeus.

Consta que a ordem das mortes na cisterna de Jotapata foi definida por sorteio. E se coubesse a ele, como comandante, esta decisão? Poderia definir quem deveria ser o primeiro executado de maneira que ao final restasse apenas ele. Este problema ficou conhecido como Problema de Josephus ou Roleta Romana.

Descrição

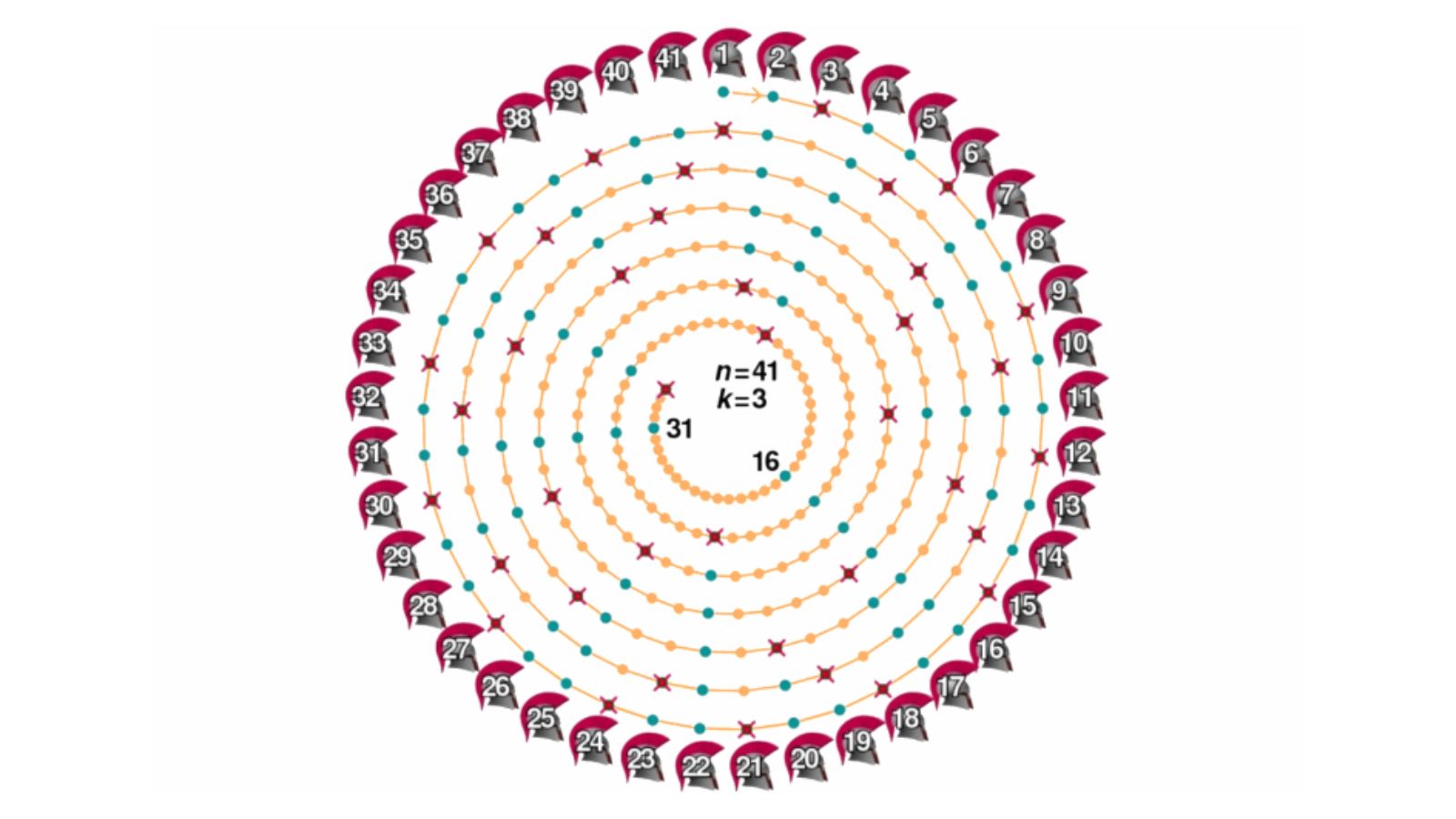
Em resumo: a partir de um certo número de pessoas organizadas sobre um círculo, uma direção e um ponto inicial, a próxima pessoa viva executa o seu vizinho e assim sucessivamente até que só reste um de pé. Por exemplo, suponhamos que haja 6 pessoas sobre um desenho de um relógio circular de ponteiros localizadas nas posições correspondentes à marcação de 2, 4, 6, 8, 10 ou 12 horas (ponteiro pequeno). Assumindo que o processo se inicie pela pessoa que está na posição 2h teríamos:

Sequência: 2 mata 4, 6 mata 8, 10 mata 12, continuando, 2 mata 6, 10 mata 2. Restou vivo aquele que iniciou o processo na posição correspondente a 2 horas.

A partir desta situação, generaliza-se um problema matemático: Qual seria a posição P do sobrevivente em um círculo com N pessoas se o processo se inicia na posição 1? Abaixo, uma simulação das execuções.

Saiba mais
O que fizemos foi construir o caso geral, uma solução completa e muito interessante com a demonstração por indução foi feita por  Felippe Calsavara Gonçalves e Fernando Pereira de Souza no trabalho O PROBLEMA DE FLAVIUS JOSEPHUS na revista Colloquium Exactarum, Vol.10 N.3 e pode ser encontrado no link: aqui.

Como fazer em casa / na escola

Uma forma de tentar estudar as possíveis soluções do problema na escola é com brincadeiras de roda. Você pode dispor os alunos em roda e numerá-los em sentido anti-horário. Se a roda for feita com os alunos em pé, aqueles que forem sendo “eliminados” podem se abaixar. No caso da roda feita com alunos sentados no chão ou em cadeiras, os “eliminados” podem se deitar no chão ou sobre as pernas, dependendo do caso.

Daí, começando sempre com o número 1, cada aluno ainda “em jogo” “elimina” o próximo aluno “em jogo” disponível e assim sucessivamente até que reste apenas um, repetindo o ciclo quando for o caso.

Para se chegar a alguma conclusão, é interessante variar a quantidade de participantes o máximo possível (de acordo com a quantidade de alunos disponível) e ir observando quem sobra “vivo” ao final.

Em casa o problema também pode ser estudado através de desenhos de sequências numéricas em números onde vamos riscando os números eliminados e isso nos possibilita testar quem sobra vivo para quantidades diferentes de pessoas e tentar chegar num padrão que resolva o problema.